Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
[Preprint]. 2021 Apr 5:arXiv:2104.01958v2.

A Generalized Unscented Transformation for Probability Distributions

Donald Ebeigbe  1 , Tyrus Berry  2 , Michael M Norton  1 , Andrew J Whalen  1   3 , Dan Simon  4 , Timothy Sauer  2 , Steven J Schiff  5
Affiliations

A Generalized Unscented Transformation for Probability Distributions

Donald Ebeigbe et al. ArXiv. .

Update in

Abstract

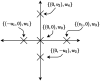
The unscented transform uses a weighted set of samples called sigma points to propagate the means and covariances of nonlinear transformations of random variables. However, unscented transforms developed using either the Gaussian assumption or a minimum set of sigma points typically fall short when the random variable is not Gaussian distributed and the nonlinearities are substantial. In this paper, we develop the generalized unscented transform (GenUT), which uses 2n+1 sigma points to accurately capture up to the diagonal components of the skewness and kurtosis tensors of most probability distributions. Constraints can be analytically enforced on the sigma points while guaranteeing at least second-order accuracy. The GenUT uses the same number of sigma points as the original unscented transform while also being applicable to non-Gaussian distributions, including the assimilation of observations in the modeling of infectious diseases such as coronavirus (SARS-CoV-2) causing COVID-19.

Keywords: Estimation; Infectious disease; Kalman filtering; Probability distributions; Unscented transform.

PubMed Disclaimer

Figures

Fig. 1.
Fig. 1.
Samples chosen for a one-dimensional distribution for the GenUT. The locations and weights of the sigma points are determined by the moments of the probability distribution.
Fig. 2.
Fig. 2.
Samples chosen for a two-dimensional distribution for the GenUT. The locations and weights of the sigma points are determined by the moments of the probability distribution.
Fig. 3.
Fig. 3.
(a) Locations of sigma points for the unconstrained (Algorithm 1), truncated, and constrained (Algorithm 2) sigma points. (b) Mean and covariance of the unconstrained (Algorithm 1), truncated, and constrained (Algorithm 2) sigma points.
Fig. 4.
Fig. 4.
(a) Moments of y = sin(x) when x is a Poisson random variable. (b) Moments of y = sin(x) when x is a Weibull random variable.
See this image and copyright information in PMC

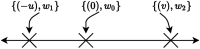
References

    1. Simon D., Optimal state estimation: Kalman, H infinity, and nonlinear approaches. John Wiley & Sons, 2006.
    1. Kandepu R., Imsland L., and Foss B. A., “Constrained state estimation using the unscented kalman filter,” in 16th Mediterranean Conference on Control and Automation, 2008, pp. 1453–1458.
    1. Izanloo R., Fakoorian S. A., Yazdi H. S., and Simon D., “Kalman filtering based on the maximum correntropy criterion in the presence of non-gaussian noise,” in 50th Annual Conference on Information Science and Systems (CISS), 2016, pp. 530–535.
    1. Gustafsson F. and Hendeby G., “Some relations between extended and unscented kalman filters,” IEEE Transactions on Signal Processing, vol. 60, no. 2, pp. 545–555, 2011.
    1. Evensen G., “Sequential data assimilation with a nonlinear quasigeostrophic model using monte carlo methods to forecast error statistics,” Journal of Geophysical Research: Oceans, vol. 99, no. C5, pp. 10143–10162, 1994.

Publication types

LinkOut - more resources