Frequency locking in auditory hair cells: Distinguishing between additive and parametric forcing

Abstract

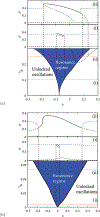
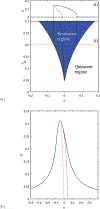
- The auditory system displays remarkable sensitivity and frequency discrimination, attributes shown to rely on an amplification process that involves a mechanical as well as a biochemical response. Models that display proximity to an oscillatory onset (also known as Hopf bifurcation) exhibit a resonant response to distinct frequencies of incoming sound, and can explain many features of the amplification phenomenology. To understand the dynamics of this resonance, frequency locking is examined in a system near the Hopf bifurcation and subject to two types of driving forces: additive and parametric. Derivation of a universal amplitude equation that contains both forcing terms enables a study of their relative impact on the hair cell response. In the parametric case, although the resonant solutions are 1 : 1 frequency locked, they show the coexistence of solutions obeying a phase shift of π, a feature typical of the 2 : 1 resonance. Different characteristics are predicted for the transition from unlocked to locked solutions, leading to smooth or abrupt dynamics in response to different types of forcing. The theoretical framework provides a more realistic model of the auditory system, which incorporates a direct modulation of the internal control parameter by an applied drive. The results presented here can be generalized to many other media, including Faraday waves, chemical reactions, and elastically driven cardiomyocytes, which are known to exhibit resonant behavior.

Keywords: Biological and medical physics; Elasticity theory; Nonlinear dynamics and chaos; Sensory systems; auditory; olfactation; tactile; taste; visual.

Fig. 1:

(Colour online) Domains describing the 1 : 1 frequency-locked (resonant) and unlocked oscillations above the Hopf bifurcation (μ > 0), in a parameter space of detuning (ν) and forcing magnitudes for (a) parametric forcing, γ_p > 0, γ_a = 0 and (b) additive forcing, γ_p = 0, γ_a > 0. The bottom panel describes the resonant region (shaded area), while the top panels describe the amplitudes of resonant solutions and unlocked oscillations (light dashed lines) at two distinct γ values (γ_p = 0.1, 0.25, γ_a = 0.005, 0.08) as a function of ν; solid lines mark stable solutions, and the dashed line in the bottom panel of (a) marks the locus of points at which the nontrivial solutions bifurcate. Equation (3) was solved with parameters: μ = 0.1 and (a) ω_c = 0.5, (b) ω_c = 1.

Fig. 2:

(Colour online) (a) 1 : 1 frequency-locked (resonant) domain and unlocked oscillations below the Hopf bifurcation (μ < 0), in a parameter space of detuning (ν) and forcing magnitudes for parametric forcing, γ_p > 0, γ_a = 0. The bottom panel describes the resonant region (shaded area), while the top panel describes a typical behavior at a specific γ (γ_p = 0.2) value as a function of ν; solid lines mark stable solutions, and the dashed line in the bottom panel marks the locus of subcritical bifurcation onsets for the nontrivial solution. (b) A typical amplitude dependence at a specific γ value (γ_a = 0.05) as a function of ν, for the additive case (dark line), with a superimposed parametric case (light line) that is taken from (a) at slice (i). Equation (3) was solved with parameters: (a) μ = −0.005, ω_c = 0.5 and (b) μ = −0.1, ω_c = 1.