Transition from growth to decay of an epidemic due to lockdown
- PMID: 33864787
- PMCID: PMC8390909
- DOI: 10.1016/j.bpj.2021.04.004
Transition from growth to decay of an epidemic due to lockdown
Abstract
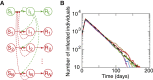
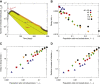
We study the transition of an epidemic from growth phase to decay of the active infections in a population when lockdown health measures are introduced to reduce the probability of disease transmission. Although in the case of uniform lockdown, a simple compartmental model would indicate instantaneous transition to decay of the epidemic, this is not the case when partially isolated active clusters remain with the potential to create a series of small outbreaks. We model this using the Gillespie stochastic simulation algorithm based on a connected set of stochastic susceptible-infected-removed/recovered networks representing the locked-down majority population (in which the reproduction number is less than 1) weakly coupled to a large set of small clusters in which the infection may propagate. We find that the presence of such active clusters can lead to slower than expected decay of the epidemic and significantly delayed onset of the decay phase. We study the relative contributions of these changes, caused by the active clusters within the population, to the additional total infected population. We also demonstrate that limiting the size of the inevitable active clusters can be efficient in reducing their impact on the overall size of the epidemic outbreak. The deceleration of the decay phase becomes apparent when the active clusters form at least 5% of the population.
Copyright © 2021 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures


Similar articles
-
Some properties of a simple stochastic epidemic model of SIR type.Math Biosci. 2007 Jul;208(1):76-97. doi: 10.1016/j.mbs.2006.09.018. Epub 2006 Oct 11. Math Biosci. 2007. PMID: 17173939 Free PMC article.
-
Modelling with SPEED: a Stochastic Predictor of Early Epidemic Detection.J Theor Biol. 2025 Jun 21;607:112120. doi: 10.1016/j.jtbi.2025.112120. Epub 2025 Apr 4. J Theor Biol. 2025. PMID: 40189138
-
Early detection of cholera epidemics to support control in fragile states: estimation of delays and potential epidemic sizes.BMC Med. 2020 Dec 15;18(1):397. doi: 10.1186/s12916-020-01865-7. BMC Med. 2020. PMID: 33317544 Free PMC article.
-
Network epidemic models with two levels of mixing.Math Biosci. 2008 Mar;212(1):69-87. doi: 10.1016/j.mbs.2008.01.001. Epub 2008 Jan 11. Math Biosci. 2008. PMID: 18280521
-
SEIRS epidemics with disease fatalities in growing populations.Math Biosci. 2018 Feb;296:45-59. doi: 10.1016/j.mbs.2017.11.006. Epub 2017 Nov 16. Math Biosci. 2018. PMID: 29155133 Review.
Cited by
-
The study of psychological traits among Chinese college students during the COVID-19 campus lockdown.Front Psychol. 2022 Nov 21;13:1051770. doi: 10.3389/fpsyg.2022.1051770. eCollection 2022. Front Psychol. 2022. PMID: 36478938 Free PMC article.
-
Challenges in the mathematical modeling of the spatial diffusion of SARS-CoV-2 in Chile.Math Biosci Eng. 2025 May 27;22(7):1680-1721. doi: 10.3934/mbe.2025062. Math Biosci Eng. 2025. PMID: 40676990 Free PMC article.
-
Effects of interpersonal sensitivity on depressive symptoms in postgraduate students during the COVID-19 pandemic: Psychological capital and sleep quality as mediators.Front Psychiatry. 2023 Apr 6;14:1100355. doi: 10.3389/fpsyt.2023.1100355. eCollection 2023. Front Psychiatry. 2023. PMID: 37091716 Free PMC article.
References
-
- Anderson R., May R.M. Oxford University Press; Oxford, UK: 1991. Infectious Diseases of Humans: Dynamics and Control.
-
- Ferguson N.M., Cummings D.A., Burke D.S. Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature. 2005;437:209–214. - PubMed
-
- Ferguson, N., D. Laydon, …, A. Ghani. 2020. Report 9: impact of non-pharmaceutical interventions (npis) to reduce covid-19 mortality and healthcare demand. Spiral, Imperial College London’s repository, pp. 1–20.
-
- Kermack W., McKendrick A. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A. 1927;115:700–721.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

