Determining electron-nucleus distances and Fermi contact couplings from ENDOR spectra
- PMID: 33875997
- PMCID: PMC8738844
- DOI: 10.1039/d1cp00229e
Determining electron-nucleus distances and Fermi contact couplings from ENDOR spectra
Abstract
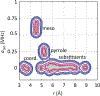
The hyperfine coupling between an electron spin and a nuclear spin depends on the Fermi contact coupling aiso and, through dipolar coupling, the distance r between the electron and the nucleus. It is measured with electron-nuclear double resonance (ENDOR) spectroscopy and provides insight into the electronic and spatial structure of paramagnetic centers. The analysis and interpretation of ENDOR spectra is commonly done by ordinary least-squares fitting. As this is an ill-posed, inverse mathematical problem, this is challenging, in particular for spectra that show features from several nuclei or where the hyperfine coupling parameters are distributed. We introduce a novel Tikhonov-type regularization approach that analyzes an experimental ENDOR spectrum in terms of a complete non-parametric distribution over r and aiso. The approach uses a penalty function similar to the cross entropy between the fitted distribution and a Bayesian prior distribution that is derived from density functional theory calculations. Additionally, we show that smoothness regularization, commonly used for a similar purpose in double electron-electron resonance (DEER) spectroscopy, is not suited for ENDOR. We demonstrate that the novel approach is able to identify and quantitate ligand protons with electron-nucleus distances between 4 and 9 Å in a series of vanadyl porphyrin compounds.
Conflict of interest statement
Conflicts of interest
There are no conflicts to declare.
Figures

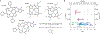
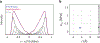
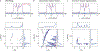

Similar articles
-
Electron-mediating Cu(A) centers in proteins: a comparative high field (1)H ENDOR study.J Am Chem Soc. 2002 Jul 10;124(27):8152-62. doi: 10.1021/ja012514j. J Am Chem Soc. 2002. PMID: 12095361
-
Coordination of the Rieske-type [2Fe-2S] cluster of the terminal iron-sulfur protein of Pseudomonas putida benzene 1,2-dioxygenase, studied by one- and two-dimensional electron spin-echo envelope modulation spectroscopy.Biochemistry. 1995 Dec 26;34(51):16533-42. doi: 10.1021/bi00051a001. Biochemistry. 1995. PMID: 8527426
-
Electron nuclear double resonance study of the Mn2+ environs in the oxalate-ATP complex of pyruvate kinase.Biochemistry. 1993 Aug 3;32(30):7799-810. doi: 10.1021/bi00081a027. Biochemistry. 1993. PMID: 8394116
-
Bayesian optimization to estimate hyperfine couplings from 19F ENDOR spectra.J Magn Reson. 2023 Aug;353:107491. doi: 10.1016/j.jmr.2023.107491. Epub 2023 May 31. J Magn Reson. 2023. PMID: 37301045
-
Spin distribution and the location of protons in paramagnetic proteins.Annu Rev Biophys Biomol Struct. 2004;33:441-68. doi: 10.1146/annurev.biophys.33.110502.140344. Annu Rev Biophys Biomol Struct. 2004. PMID: 15139821 Review.
Cited by
-
Bidentate Substrate Binding Mode in Oxalate Decarboxylase.Molecules. 2024 Sep 17;29(18):4414. doi: 10.3390/molecules29184414. Molecules. 2024. PMID: 39339409 Free PMC article.
-
Frequency and time domain 19F ENDOR spectroscopy: role of nuclear dipolar couplings to determine distance distributions.Phys Chem Chem Phys. 2025 Jan 15;27(3):1415-1425. doi: 10.1039/d4cp04443f. Phys Chem Chem Phys. 2025. PMID: 39696963 Free PMC article.
References
-
- Feher G, Physical Review, 1956, 103, 834–835.
-
- Hyde JS and Maki AH, The Journal of Chemical Physics, 1964, 40, 3117–3118.
-
- Hyde JS, The Journal of Chemical Physics, 1965, 43, 1806–1818.
-
- Harmer JR, eMagRes, John Wiley & Sons, Ltd, Chichester, UK, 2016, pp. 1493–1514.
-
- Davies ER, Physics Letters A, 1974, 47, 1–2.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

