Prediction of Covid-19 spreading and optimal coordination of counter-measures: From microscopic to macroscopic models to Pareto fronts

Abstract

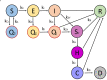
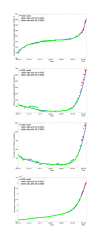
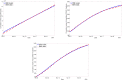
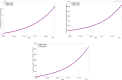
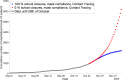
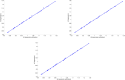
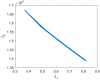
The Covid-19 disease has caused a world-wide pandemic with more than 60 million positive cases and more than 1.4 million deaths by the end of November 2020. As long as effective medical treatment and vaccination are not available, non-pharmaceutical interventions such as social distancing, self-isolation and quarantine as well as far-reaching shutdowns of economic activity and public life are the only available strategies to prevent the virus from spreading. These interventions must meet conflicting requirements where some objectives, like the minimization of disease-related deaths or the impact on health systems, demand for stronger counter-measures, while others, such as social and economic costs, call for weaker counter-measures. Therefore, finding the optimal compromise of counter-measures requires the solution of a multi-objective optimization problem that is based on accurate prediction of future infection spreading for all combinations of counter-measures under consideration. We present a strategy for construction and solution of such a multi-objective optimization problem with real-world applicability. The strategy is based on a micro-model allowing for accurate prediction via a realistic combination of person-centric data-driven human mobility and behavior, stochastic infection models and disease progression models including micro-level inclusion of governmental intervention strategies. For this micro-model, a surrogate macro-model is constructed and validated that is much less computationally expensive and can therefore be used in the core of a numerical solver for the multi-objective optimization problem. The resulting set of optimal compromises between counter-measures (Pareto front) is discussed and its meaning for policy decisions is outlined.

Fig 1. Semi-logarithmic plot of numbers of people showing symptoms for Berlin.

Results of a single ABM simulation run (blue solid line) in comparison to official RKI observation data (red dots: reference date; green dots: reporting date).

Fig 2. Schematic illustration of our model for the spread of Covid-19 in Berlin.

Fig 3. Predictions based on the ODE model for the spread of Covid-19 in Berlin: Cumulative number of deceased (top, left), number of hospital beds occupied (top, right), number of ICU beds occupied (bottom, left), and cumulative number of positively tested persons (bottom, right).

Green dots: Real-life data used for fitting the ODE model. Blue solid line: Solution of optimally fitted ODE model. Red dots: Real-life data used for validation.

Fig 4. Optimal ODE fit for the ABM data simulating 100% school closures, 100% mask compliance and 100% contact tracing.

Fig 5. Optimal ODE fit for the ABM data simulating no school closures, no mask compliance and no contact tracing.

Fig 6. The ODE fit for the ABM data simulating 100% school closures, 100% mask compliance and 100% contact tracing. This time, only k_E was used to fit the data.

Fig 7. Difference in the ABM predictions of hospitalization numbers in Berlin when different counter-measures are used.

The grey line shows the underlying observation data. On October 27, the difference in the counter-measures takes effect. The blue line (c = (0, 0, 0)) and the red line (c = (1, 1, 1)) show the resulting different projections for November.

Fig 8. Polynomial regression function for k_E with different degrees.

The plots show the result when polynomials of degree 2, 3, or 4, respectively, are used. The accuracy does not improve significantly if a higher degree than 2 is used.

Fig 9. Box covering of Pareto front shown from two different perspectives.

Only the box centers are displayed (level 1 (blue dots) and level 3 (red dots)).

Fig 10. Values of the two objective functions J₁ and J₂ along the Pareto front displayed in Fig 9 plotted against each other.