Collective and synchronous dynamics of photonic spiking neurons

Abstract

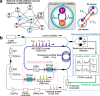
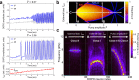
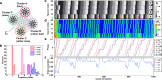
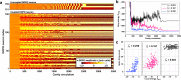
Nonlinear dynamics of spiking neural networks have recently attracted much interest as an approach to understand possible information processing in the brain and apply it to artificial intelligence. Since information can be processed by collective spiking dynamics of neurons, the fine control of spiking dynamics is desirable for neuromorphic devices. Here we show that photonic spiking neurons implemented with paired nonlinear optical oscillators can be controlled to generate two modes of bio-realistic spiking dynamics by changing optical-pump amplitude. When the photonic neurons are coupled in a network, the interaction between them induces an effective change in the pump amplitude depending on the order parameter that characterizes synchronization. The experimental results show that the effective change causes spontaneous modification of the spiking modes and firing rates of clustered neurons, and such collective dynamics can be utilized to realize efficient heuristics for solving NP-hard combinatorial optimization problems.

Fig. 1. Experimental setup of a DOPO neural network.

a 240-node artificial neural network composed of 480 DOPOs with antisymmetric couplings ($J_{vw}=-J_{wv}$). b Schematic diagram based on time-domain multiplexing in a 1-km fiber-ring cavity. PPLN, periodically poled lithium-niobate; PMF, polarization-maintaining fiber; IM, intensity modulator; EDFA, erbium-doped-fiber amplifier; FPGA, field-programmable gate array.

Fig. 2. Class-I and II spiking modes of a DOPO neuron.

a Time evolutions of $v$- and $w$-DOPOs (blue and gray lines) with constant pump amplitudes ($\tilde{P}$ = 0.57 and 1.36) and an external bias increased linearly with time. b Phase diagram of the DOPO neuron in the parameter space of $P$ and $I_{\mathrm{ext}}$. The color map represents spiking frequencies calculated by numerical simulations. Red and blue dots obtained by linear stability analysis represent points where the Andronov–Hopf (AH) bifurcation and saddle-node bifurcation on a limit cycle (SNLC) occur, so they characterize class-II and class-I neurons, respectively. c Experimental results of tomographic measurement of spiking frequencies along lines A, B, and C in (b). The color map represents Fourier signals of time evolutions of DOPO amplitudes. Cyan points are firing rates estimated by adding up the number of spikes.

Fig. 3. Synchronization experiment using clustered Kuramoto models.

a Structure of DOPO-neuron network consisting of four clusters of 15 neurons. b Firing-rate distribution of 60 neurons. For $J_k=0$, the distribution is spread as designed on the basis of pump amplitude. c Time evolutions of phase ${\theta }_i$ of the ith DOPO neuron with coupling of $\widetilde{J_k}$ = 0.075, where ${\theta }_i$ is an angle defined in the $v$-$w$ plane of the coupled DOPOs. d Phase change $△{\theta }_i$ per four cavity circulations. e Phase ${\theta }_i$of a sampled neuron in each cluster. f Order parameter $r$ for each cluster and for all 60 neurons. Synchronization can be characterized by $r~1$.

Fig. 4. Spiking dynamics when solving a 150-node Ising problem.

a Time evolutions of $v$-DOPO amplitudes with couplings of $\widetilde{J_k}$ = 0.250 (lower) and without coupling (top). Pump amplitudes increase linearly with time. b Time evolutions of Ising energy for $\widetilde{J_k}$ = 0.083, 0.167, and 0.250. Strong couplings give the best-known solution. c Relationship between local energy and firing rate. Firing rate and local energy are positively correlated with strong couplings, suggesting that energetically unstable neurons have high firing rate due to the self-tuning effect of the spiking mode.