Spatial scales in human movement between reservoirs of infection

Abstract

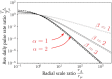
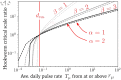
The life cycle of parasitic organisms that are the cause of much morbidity in humans often depend on reservoirs of infection for transmission into their hosts. Understanding the daily, monthly and yearly movement patterns of individuals between reservoirs is therefore of great importance to implementers of control policies seeking to eliminate various parasitic diseases as a public health problem. This is due to the fact that the underlying spatial extent of the reservoir of infection, which drives transmission, can be strongly affected by inputs from external sources, i.e., individuals who are not spatially attributed to the region defined by the reservoir itself can still migrate and contribute to it. In order to study the importance of these effects, we build and examine a novel theoretical model of human movement between spatially-distributed focal points for infection clustered into regions defined as 'reservoirs of infection'. Using our model, we vary the spatial scale of human moment defined around focal points and explicitly calculate how varying this definition can influence the temporal stability of the effective transmission dynamics - an effect which should strongly influence how control measures, e.g., mass drug administration (MDA), define evaluation units (EUs). Considering the helminth parasites as our main example, by varying the spatial scale of human movement, we demonstrate that a critical scale exists around infectious focal points at which the migration rate into their associated reservoir can be neglected for practical purposes. This scale varies by species and geographic region, but is generalisable as a concept to infectious reservoirs of varying spatial extents and shapes. Our model is designed to be applicable to a very general pattern of infectious disease transmission modified by the migration of infected individuals between clustered communities. In particular, it may be readily used to study the spatial structure of hosts for macroparasites with temporally stationary distributions of infectious focal point locations over the timescales of interest, which is viable for the soil-transmitted helminths and schistosomes. Additional developments will be necessary to consider diseases with moving reservoirs, such as vector-born filarial worm diseases.

Keywords: Control policies; Mathematical models; Monitoring and evaluation; Spatial infection model.

Fig. 1

Illustration of the transmission dynamics of human helminth infections via a defined focal point.

Fig. 2

Left column: The cumulative number of buildings (vertical axis) below a given radial distance (horizontal axis) from sample locations in Malawi, Benin and the Ivory Coast obtained from the high resolution settlement layer dataset generated by the Facebook Connectivity Lab (High Resolution Settlement Layer (HRSL), 2016). Lines for different constant $\alpha$ and $r_{\mu }$ values are provided only as rough indicators for comparison. Right column: The sample mean lines and root-mean-square deviation (RMSD) shaded regions of the power law index $\alpha$ plotted against radial distance in each case. The RMSD was calculated by computing discrete derivatives between log-frequency bins as a function of log-radial distance. In each country, the collection of sample locations was randomly drawn from: the central region of Malawi, including Lilongwe; the wide northern region of Benin, spanning between Kandi and Djougou; and a wide central region of the Ivory Coast, including Yamoussoukro.

Fig. 3

Plots of the marginal probability density $p(r\text{;}\alpha ,\beta ,r_{\mu })$ as a function of radial distance (in units of km) generated using Eq. (5) for a range of $\alpha ,\beta$ and $r_{\mu }$ values for comparison.

Fig. 4

The binned frequency of ${10}^4$ individuals simulated to travel a between two buildings (solid lines) whose locations correspond to data from the same regions of each country as in Fig. 2 (where some globally-applied uniform random point density thinning has been used to reduce computational load of exploring the distribution tails). This corresponds to the same marginalised jump probability density as Eq. (5) but instead of using a geometric power-law given by Eq. (1) we have implemented our single jumps on real-world map data (with exponential jump distributions each with a scale drawn from Eq. (4)). For comparison, we have also plotted some jump probabilities calculated using Eq. (5) with $\alpha =1$ (dashed lines) and $\alpha =2$ (dotted lines). In all cases we have fixed $\beta =2$.

Fig. 5

Numerical plots of the distance distributions generated by the multi-jump processes introduced in Section 3.1 with randomly-directed (left panel) and in Section 3.2 with unidirectional jumps (right panel). In the left panel, a population of $5\times {10}^4$ individuals following the process defined by Eq. (6) have been drawn (drawing from Eq. (4) for their jump scale predispositions) and the binned frequency of the total distance evaluated at the end of the day with jump rates of $\mathcal{J}=1,20$ per day (in red and black lines, respectively), $\alpha =1$ and $\beta =1,2,3$ as indicated by the increasing opacity within each triplet of lines. In the right panel, the marginal probability density given by Eq. (15) is depicted with jump rates of $\mathcal{J}=1,10$ per day (in red and black lines, respectively), $\alpha =1$ and $\beta =1,2,3$ as indicated by the increasing opacity within each triplet of lines.

Fig. 6

A diagram of real map data (based on buildings in central Malawi) and a zoomed illustration which indicate the coarse-graining procedure of Eq. (21) – in which the black arrows are ‘removed’. Arrows depict individual movements from households (grey hollow dots on the right hand side zoomed illustration) to focal points of infection (black hollow dots on the right hand side zoomed illustration) where black arrows on both the map and its zoomed counterpart correspond to jumps over a radial distance $r<r_{\mathrm{\Lambda }}$ (where $r_{\mathrm{\Lambda }}$ is the spatial coarse-graining scale) and red arrows correspond to jumps over a radial distance $r⩾r_{\mathrm{\Lambda }}$. On the left hand side zoomed illustration we see the emergence of the spatially coarse-grained reservoir network ‘nodes’ (nodes are neither drawn to scale nor have geometrically-accurate reservoir spatial shapes) connected by red migratory ‘links’ in time.

Fig. 7

The spatially coarse-grained average daily pulse rate $T_{\mathrm{\Lambda }}$ into a focal point of infection as a fraction of its value $T_{\mu }$ from individuals arriving a distance of $r_{\mu }$ or greater away. This value is plotted as a function of the radial coarse-graining scale ratio $r_{\mathrm{\Lambda }}/r_{\mu }$ used. The relationship is given by Eq. (22) for a range of $\alpha$ and $\beta$ power-law parameters.

Fig. 8

The critical spatial scale as a ratio $r_{\mathrm{\Lambda }}^{\ast }$ at which $T_{\mathrm{\Lambda }}^{\ast }=d_{\mathrm{res}}$, for hookworm – where $d_{\mathrm{res}}\simeq 0.071$ (Truscott et al., 2016) – plotted as a ratio of $r_{\mu }$. The value of this scale is shown against the value of the average daily pulse rate $T_{\mu }$ at or above $r_{\mu }$. We have used Eq. (22) to generate this relationship with a (bisection) root-finding algorithm.