An Overcomplete Approach to Fitting Drift-Diffusion Decision Models to Trial-By-Trial Data
- PMID: 33898982
- PMCID: PMC8064018
- DOI: 10.3389/frai.2021.531316
An Overcomplete Approach to Fitting Drift-Diffusion Decision Models to Trial-By-Trial Data
Abstract
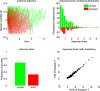
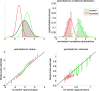
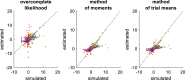
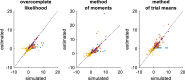
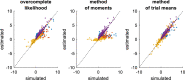
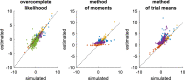
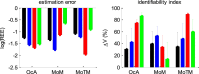
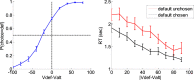
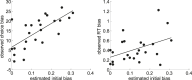
Drift-diffusion models or DDMs are becoming a standard in the field of computational neuroscience. They extend models from signal detection theory by proposing a simple mechanistic explanation for the observed relationship between decision outcomes and reaction times (RT). In brief, they assume that decisions are triggered once the accumulated evidence in favor of a particular alternative option has reached a predefined threshold. Fitting a DDM to empirical data then allows one to interpret observed group or condition differences in terms of a change in the underlying model parameters. However, current approaches only yield reliable parameter estimates in specific situations (c.f. fixed drift rates vs drift rates varying over trials). In addition, they become computationally unfeasible when more general DDM variants are considered (e.g., with collapsing bounds). In this note, we propose a fast and efficient approach to parameter estimation that relies on fitting a "self-consistency" equation that RT fulfill under the DDM. This effectively bypasses the computational bottleneck of standard DDM parameter estimation approaches, at the cost of estimating the trial-specific neural noise variables that perturb the underlying evidence accumulation process. For the purpose of behavioral data analysis, these act as nuisance variables and render the model "overcomplete," which is finessed using a variational Bayesian system identification scheme. However, for the purpose of neural data analysis, estimates of neural noise perturbation terms are a desirable (and unique) feature of the approach. Using numerical simulations, we show that this "overcomplete" approach matches the performance of current parameter estimation approaches for simple DDM variants, and outperforms them for more complex DDM variants. Finally, we demonstrate the added-value of the approach, when applied to a recent value-based decision making experiment.
Keywords: DDM; computational modeling; decision making; neural noise; variational bayes.
Copyright © 2021 Feltgen and Daunizeau.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures



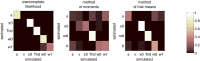
Similar articles
-
A Bayesian Reformulation of the Extended Drift-Diffusion Model in Perceptual Decision Making.Front Comput Neurosci. 2017 May 11;11:29. doi: 10.3389/fncom.2017.00029. eCollection 2017. Front Comput Neurosci. 2017. PMID: 28553219 Free PMC article.
-
Value certainty in drift-diffusion models of preferential choice.Psychol Rev. 2023 Apr;130(3):790-806. doi: 10.1037/rev0000329. Epub 2021 Oct 25. Psychol Rev. 2023. PMID: 34694845
-
A flexible framework for simulating and fitting generalized drift-diffusion models.Elife. 2020 Aug 4;9:e56938. doi: 10.7554/eLife.56938. Elife. 2020. PMID: 32749218 Free PMC article.
-
A practical introduction to using the drift diffusion model of decision-making in cognitive psychology, neuroscience, and health sciences.Front Psychol. 2022 Dec 9;13:1039172. doi: 10.3389/fpsyg.2022.1039172. eCollection 2022. Front Psychol. 2022. PMID: 36571016 Free PMC article. Review.
-
Computational approaches to modeling gambling behaviour: Opportunities for understanding disordered gambling.Neurosci Biobehav Rev. 2023 Apr;147:105083. doi: 10.1016/j.neubiorev.2023.105083. Epub 2023 Feb 8. Neurosci Biobehav Rev. 2023. PMID: 36758827 Review.
Cited by
-
Evidence or Confidence: What Is Really Monitored during a Decision?Psychon Bull Rev. 2023 Aug;30(4):1360-1379. doi: 10.3758/s13423-023-02255-9. Epub 2023 Mar 14. Psychon Bull Rev. 2023. PMID: 36917370 Free PMC article. Review.
-
Flexible and efficient simulation-based inference for models of decision-making.Elife. 2022 Jul 27;11:e77220. doi: 10.7554/eLife.77220. Elife. 2022. PMID: 35894305 Free PMC article.
-
Cognitive effort and active inference.Neuropsychologia. 2023 Jun 6;184:108562. doi: 10.1016/j.neuropsychologia.2023.108562. Epub 2023 Apr 18. Neuropsychologia. 2023. PMID: 37080424 Free PMC article.
References
-
- Beal M. J. (2003). Variational algorithms for approximate Bayesian inference/. PhD Thesis. London: University College London.
-
- Boehm U., Annis J., Frank M. J., Hawkins G. E., Heathcote A., Kellen D., et al. (2018). Estimating across-trial variability parameters of the diffusion decision model: expert advice and recommendations. J. Math. Psychol. 87, 46–75. 10.1016/j.jmp.2018.09.004 - DOI
LinkOut - more resources
Full Text Sources
Other Literature Sources

