Communication consumes 35 times more energy than computation in the human cortex, but both costs are needed to predict synapse number

Abstract

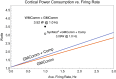
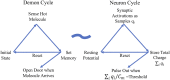
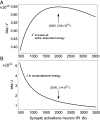
Darwinian evolution tends to produce energy-efficient outcomes. On the other hand, energy limits computation, be it neural and probabilistic or digital and logical. Taking a particular energy-efficient viewpoint, we define neural computation and make use of an energy-constrained computational function. This function can be optimized over a variable that is proportional to the number of synapses per neuron. This function also implies a specific distinction between adenosine triphosphate (ATP)-consuming processes, especially computation per se vs. the communication processes of action potentials and transmitter release. Thus, to apply this mathematical function requires an energy audit with a particular partitioning of energy consumption that differs from earlier work. The audit points out that, rather than the oft-quoted 20 W of glucose available to the human brain, the fraction partitioned to cortical computation is only 0.1 W of ATP [L. Sokoloff, Handb. Physiol. Sect. I Neurophysiol. 3, 1843-1864 (1960)] and [J. Sawada, D. S. Modha, "Synapse: Scalable energy-efficient neurosynaptic computing" in Application of Concurrency to System Design (ACSD) (2013), pp. 14-15]. On the other hand, long-distance communication costs are 35-fold greater, 3.5 W. Other findings include 1) a [Formula: see text]-fold discrepancy between biological and lowest possible values of a neuron's computational efficiency and 2) two predictions of N, the number of synaptic transmissions needed to fire a neuron (2,500 vs. 2,000).

Keywords: bits per joule; brain energy consumption; energy-efficient; neural computation; optimal computation.

Fig. 1.

Computation costs little compared to communication. Communication alone accounts for more than two-thirds of the available 4.94 ATP-W (Table 1), with slightly more consumption due to WM than to GM (big pie chart). Computation, the smallest consumer, is subpartitioned by the two ionotropic glutamate receptors (bar graph). $SynMo{d}^{+}$ includes astrocytic costs, process extension, process growth, axo- and dendro-plasmic transport of the membrane building blocks, and time-independent housekeeping costs (although this last contributor is a very small fraction). The small pie chart subpartitions GM communication. See Results and Materials and Methods for details. WM communication includes its maintenance and myelination costs in addition to resting and action potentials.

Fig. 2.

Energy use increases linearly with average firing rate, but for reasonable rates, computation (Comp) costs much less than communication (Comm). Comparing the bottom (red) curve (GM communication costs) to the top (blue) curve (GM communication cost plus computational costs) illustrates how little computational costs increase relative to communication costs. The y-intercept value is 1.09 W for resting potential. The open circle plotting $SynMo{d}^{+}$ + GMComm + Comp adds the 1.32 W of GM $SynMo{d}^{+}$ to the 1.77 W of GMComm + Comp at 1 Hz. The solid circle, labeled WMComm + GMComm, shows the value of the combined communication cost, cortical GM at 1 Hz, and the total cortical white matter cost. See Materials and Methods for further details.

Fig. 3.

Maxwell’s demon cycle is analogous to the neuron’s computational cycle. The initial state in the demon cycle is equivalent to the neuron at rest. The demon sensing fast molecules is analogous to the synaptic activations received by the neuron. Whereas the demon uses energy to set the memory and then opens the door for a molecule, the neuron stores charge on the membrane capacitance (${\mathrm{C}}_{\mathrm{m}}$) and then pulses out once this voltage reaches threshold. Simultaneous with such outputs, both cycles then reset to their initial states and begin again. Both cycles involve energy being stored and then released into the environment. The act of the demon opening the door is ignored as an energy cost; likewise, the neuron’s computation does not include the cost of communication. Each ${\mathrm{q}}_i$ is a sample and represents the charge accumulated on the plasma membrane when synapse $i$ is activated.

Fig. 4.

Bits per joule per neuron at optimal $N$. (A) The bits per joule function, Eq. [1], is concave and reaches a maximum when $N$ is ca. 2,000. This efficiency decreases little more than 5% over a sevenfold range away from this 2,000. At this optimum there are 7.48 bits per spike. (B) The optimal $N$ implies $1.4\cdot 10^{12}$ bits per computational joule. B is calculated by changing Eq. [1]’s denominator to $E\left[T\right]N\cdot B÷\left(\mathrm{2,500}\cdot n\right)$ instead of $E\left[T\right]\left(A+N\cdot B/\mathrm{2,500}\right)÷n$.