Multifractality through Non-Markovian Stochastic Processes in the Scale Relativity Theory. Acute Arterial Occlusions as Scale Transitions

Abstract

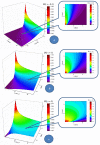
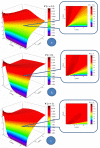
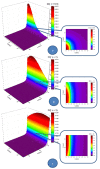
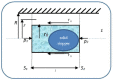
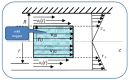
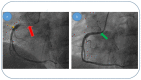
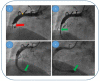
By assimilating biological systems, both structural and functional, into multifractal objects, their behavior can be described in the framework of the scale relativity theory, in any of its forms (standard form in Nottale's sense and/or the form of the multifractal theory of motion). By operating in the context of the multifractal theory of motion, based on multifractalization through non-Markovian stochastic processes, the main results of Nottale's theory can be generalized (specific momentum conservation laws, both at differentiable and non-differentiable resolution scales, specific momentum conservation law associated with the differentiable-non-differentiable scale transition, etc.). In such a context, all results are explicated through analyzing biological processes, such as acute arterial occlusions as scale transitions. Thus, we show through a biophysical multifractal model that the blocking of the lumen of a healthy artery can happen as a result of the "stopping effect" associated with the differentiable-non-differentiable scale transition. We consider that blood entities move on continuous but non-differentiable (multifractal) curves. We determine the biophysical parameters that characterize the blood flow as a Bingham-type rheological fluid through a normal arterial structure assimilated with a horizontal "pipe" with circular symmetry. Our model has been validated based on experimental clinical data.

Keywords: Bingham fluid; acute arterial occlusion; multifractality; non-Markovian stochastic process; scale relativity theory.

Figure 1

(a–c). 3D and contour plot representations of the velocity component on the Oξ for three multifractality degrees: (a) 0.3; (b) 1; and (c) 3. The velocity increases from purple to red.

Figure 2

3D and contour plot representations of the velocity component on the Oη for three multifractality degrees: (a) 0.3, (b) 1 and (c) 3. The velocity increases from purple to red.

Figure 3

3D and contour plot representations of the multifractal minimal vortex for three multifractality degrees: (a) 0.3, (b) 1 and (c) 3. The vortex field increases from purple to red.

Figure 4

Pressure gradient flow induced by ventricular inotropic force as well as by the arterial wall (hatched area) elasticity for a given zone of the blood as a Bingham-type rheological fluid through a normal arterial structure assimilated with a circular pipe. l—the length of the stopper; S₁ and S₂—the lateral surfaces of the solid stopper; p₁ and p₂—the pressures along the solid stopper; R—the radius of the artery; r₀—the radius of the solid stopper; r—a specific distance along which the velocity gradient field is manifested; ${\tau }_0$—deformation tangential unitary effort; z—the flow direction.

Figure 5

Velocity and viscosity tangential unitary effort diagrams of the blood that flows in an elastic arterial wall. R—the radius of the artery; r₀—the radius of the solid stopper; r—a specific distance along which the velocity gradient field is manifested; ${\tau }_0$—deformation tangential unitary effort; z—the flow direction; v_z0—the velocity of the solid stopper (blood moves as an apparently undistorted rigid system); v_z(r)—the velocity of the blood (normal flow).

Figure 6

(a–d). Acute thrombus formation (red arrow) in an apparently healthy artery (orange arrow) with no evidence of plaque dissection—different interventional approach stages for patient 1: (a) blood flow before thromboaspiration; (c,d) blood flow returning to normal after thromboaspiration/removal of thrombus (green arrow). (b) Explanation.

Figure 7

(a,b). Acute thrombus formation (red arrow) in an apparently healthy artery (orange arrow) with no evidence of plaque dissection—different interventional approach stages for patient 2: (a) blood flow before thromboaspiration; (b) blood flow returning to normal after thromboaspiration/removal of thrombus (green arrow).

Figure 8

(a–d). Acute thrombus formation (red arrow) in an apparently healthy artery (orange arrow) with no evidence of plaque dissection—different interventional approach stages for patient 3: (a) blood flow before thromboaspiration; (c,d) blood flow returning to normal after thromboaspiration/removal of thrombus (green arrow). (b) Explanation.