The Emergence of Sequential Buckling in Reconfigurable Hexagonal Networks Embedded into Soft Matrix

Abstract

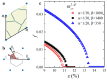
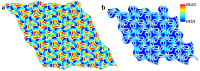
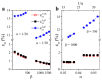
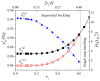
The extreme and unconventional properties of mechanical metamaterials originate in their sophisticated internal architectures. Traditionally, the architecture of mechanical metamaterials is decided on in the design stage and cannot be altered after fabrication. However, the phenomenon of elastic instability, usually accompanied by a reconfiguration in periodic lattices, can be harnessed to alter their mechanical properties. Here, we study the behavior of mechanical metamaterials consisting of hexagonal networks embedded into a soft matrix. Using finite element analysis, we reveal that under specific conditions, such metamaterials can undergo sequential buckling at two different strain levels. While the first reconfiguration keeps the periodicity of the metamaterial intact, the secondary buckling is accompanied by the change in the global periodicity and formation of a new periodic unit cell. We reveal that the critical strains for the first and the second buckling depend on the metamaterial geometry and the ratio between elastic moduli. Moreover, we demonstrate that the buckling behavior can be further controlled by the placement of the rigid circular inclusions in the rotation centers of order 6. The observed sequential buckling in bulk metamaterials can provide additional routes to program their mechanical behavior and control the propagation of elastic waves.

Keywords: buckling; elastic wave propagation; instabilities; mechanical metamaterials; reconfiguration; sequential buckling.

Figure 1

Hexagonal networks embedded into a soft deformable matrix without (a) and with (b) central inclusions. A primitive unit cell is shown in red color. Lattice vectors ${\mathit{r}}_H$ and ${\mathit{r}}_V$ couple the points on the opposite boundaries of the primitive unit cell.

Figure 2

(a) Buckling modes as a function of geometrical $\alpha$ and material $\beta$ parameters. (b) Type 2 global mode denoted by solid black squares. (c) Type 1 local mode denoted by empty red circles. (d) Type 1.5 buckling mode considered in this study denoted by blue stars. The solid continuous line corresponds to the analytical estimation of the transition zone between Type 1 and Type 2 buckling modes, i.e., Equation (1).

Figure 3

The primitive unit cell (a) and its reciprocal lattice (b) of the studied structures in the undeformed state. The gray area represents the IBZ, and the red arrows show the path along its contour. (c) Evolution of lowest branches of dispersion curves in the vicinity of the primary instability. * denotes the minimal strain ($\epsilon =0.87\%$) for which a non-trivial zero eigenvalue is found at point G. (d) Evolution of the eigenfrequencies corresponding to Type 1 and Type 2 modes with an increase in the applied strain. The Y-axis represents normalized frequency $f=\frac{\omega H}{2\pi }\sqrt{\frac{{\rho }_M}{{\mu }_M}}$.

Figure 4

Type 1 (a) and Type 2 (b) patterns associated with the first onset of buckling.

Figure 5

Dispersion curves for metamaterial with $\alpha =1/30$ and $\beta =1000$. (a) Undeformed state, (b)$\epsilon =7\%$ without reconfiguration, (c)$\epsilon =7\%$ with reconfiguration.

Figure 6

Evolution of the pattern (a–c) and corresponding dispersion curves (d–f) after the first and the second buckling for metamaterial with $\alpha =1/30$ and $\beta =1000$. (a,d) $\epsilon =3\%$, (b,e) $\epsilon =9\%$, (c,f) $\epsilon =25\%$ (updated IBZ is shown in Figure 7b). Colors denote von Mises stresses (color ranges are not synchronized for (a–c)).

Figure 7

The primitive unit cell (a) and its reciprocal lattice (b) of the studied structure after secondary buckling. The updated (virtual) IBZ contour is shown in red [66]. (c) Evolution of the lowest eigenfrequency at point K in the vicinity of primary instability.

Figure 8

Evolution of the pattern after the second buckling at $\epsilon =30\%$ (a), $\epsilon =50\%$ (b). Colors denote von Mises stresses (color ranges are not synchronized for (a, b)).

Figure 9

Dependencies of the first and the second buckling strains on material parameter $\beta$ (a) and geometrical parameter $\alpha$ (b).

Figure 10

Values of critical strains for the hexagonal networks with embedded circular inclusions.

Figure 11

Dispersion curves for the deformed composite with $\alpha =1/30, \beta =1000, \delta =0.1$ after primary buckling and $\epsilon =10\%$ for metamaterials with no inclusions (a), ${\rho }_I/{\rho }_M=1$ (b), ${\rho }_I/{\rho }_M=8$ (c). The red rectangles denote complete bandgaps for in-plane waves.