Tavis-Cummings Model with Moving Atoms

Abstract

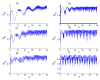
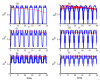
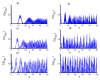
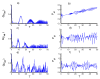
In this work, we examine a nonlinear version of the Tavis-Cummings model for two two-level atoms interacting with a single-mode field within a cavity in the context of power-law potentials. We consider the effect of the particle position that depends on the velocity and acceleration, and the coupling parameter is supposed to be time-dependent. We examine the effect of velocity and acceleration on the dynamical behavior of some quantumness measures, namely as von Neumann entropy, concurrence and Mandel parameter. We have found that the entanglement of subsystem states and the photon statistics are largely dependent on the choice of the qubit motion and power-law exponent. The obtained results present potential applications for quantum information and optics with optimal conditions.

Keywords: cat states; concurrence; entanglement; power-law potentials; statistical properties; two qubits.

Figure 1

Time evolution of the von Neumann entropy $S_N\left(T\right)$ for $\xi =\sqrt{5}$, with the case of constant two qubits–field coupling ($\vartheta =\phi =0$ and $c=\pi /2$). Figs. (a,c,e) are plotted for the field initially in the coherent states (CSs) for power-law potentials (PLPs) ($r=0$) and Figs. (b,d,f) for the field initially in the SCSs for PLPs ($r=1$). Figs. (a,b) for harmonic well potential ($k=2$), Figs. (c,d) for the triangular well ($k=1$), and Figs. (e,f) for infinite barrier ($k\to \infty$).

Figure 2

Effect of time-dependent coupling, $\ell \left(t\right)$, on the evolution of the atomic entropy $S_N\left(T\right)$ where the solid curve is for $\phi =1$ and $\vartheta =c=0$ (atomic speed effect) and the dotted red curve is for the acceleration effect ($\vartheta =\phi =1$ and $c=0$). Figs. (a,c,e) are plotted for the field initially in the coherent states (CSs) for power-law potentials (PLPs) ($r=0$) and Figs. (b,d,f) for the field initially in the SCSs for PLPs ($r=1$). Figs. (a,b) for harmonic well potential ($k=2$), Figs. (c,d) for the triangular well ($k=1$), and Figs. (e,f) for infinite barrier ($k\to \infty$).

Figure 3

Time evolution of the the concurrence $C_{AB}\left(T\right)$ for $\xi =\sqrt{5}$, with the case of constant two qubits–field coupling ($\vartheta =\phi =0$ and $c=\pi /2$). Figs. (a,c,e) are plotted for the field initially in the CSs for PLPs ($r=0$) and Figs. (b,d,f) for the field initially in the SCSs for PLPs ($r=1$) Figs. (a,b) for harmonic well potential ($k=2$), Figs. (c,d) for triangular well ($k=1$) and Figs. (e,f) for infinite well ($k\to \infty$).

Figure 4

Effect of time-dependent coupling or qubit motion, $\ell \left(t\right)$, on the evolution of the concurrence $C_{AB}\left(T\right)$ where the solid curve is for $\phi =1$ and $\vartheta =c=0$ (atomic speed effect) and the dotted red curve is for the acceleration effect as ($\vartheta =\phi =1$ and $c=0$). Figs. (a,c,e) are plotted for the field initially in the coherent states (CSs) for power-law potentials (PLPs) ($r=0$) and Figs. (b,d,f) for the field initially in the SCSs for PLPs ($r=1$). Figs. (a,b) for harmonic well potential ($k=2$), Figs. (c,d) for the triangular well ($k=1$), and Figs. (e,f) for infinite barrier ($k\to \infty$).

Figure 5

Time evolution of the Mandel parameter $P_M$ for $\xi =\sqrt{5}$ with the case of constant qubits–field coupling ($\vartheta =\phi =0$ and $c=\pi /2$). Figs. (a,c,e) are plotted for the field initially in the CSs for PLPs ($r=0$) and Figs. (b,d,f) for the field initially in the SCSs for PLPs ($r=1$). Figs. (a,b) for harmonic well potential ($k=2$), Figs. (c,d) for triangular well ($k=1$) and Figs. (e,f) for infinite well ($k\to \infty$).

Figure 6

Effect of time-dependent coupling, $\ell \left(t\right)$ on the evolution of the Mandel parameter $P_M$ where the solid curve is for $\phi =1$ and $\vartheta =c=0$ (atomic speed effect) and the dotted red curve is for the acceleration effect as ($\vartheta =\phi =1$ and $c=0$). Figs. (a,c,e) are plotted for the field initially in the coherent states (CSs) for power-law potentials (PLPs) ($r=0$) and Figs. (b,d,f) for the field initially in the SCSs for PLPs ($r=1$). Figs. (a,b) for harmonic well potential ($k=2$), Figs. (c,d) for the triangular well ($k=1$), and Figs. (e,f) for infinite barrier ($k\to \infty$).

Figure 7

Effect of qubit–qubit interaction $(D=1$) in the absence of time-dependent coupling or qubit motion ($sin(\vartheta T^2+\phi T+c)$ for $\vartheta =\phi =0$ and $c=\pi /2$) for the three CSs for PLPs studied: Figs. (a,b) for harmonic well potential ($k=2$), Figs. (c,d) for triangular well ($k=1$) and Figs. (e,f) for infinite well ($k\to \infty$).