The Consequences of Budding versus Binary Fission on Adaptation and Aging in Primitive Multicellularity
- PMID: 33924996
- PMCID: PMC8145350
- DOI: 10.3390/genes12050661
The Consequences of Budding versus Binary Fission on Adaptation and Aging in Primitive Multicellularity
Abstract
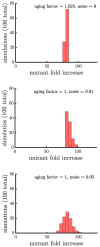
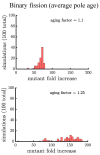
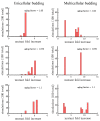
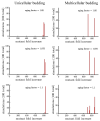
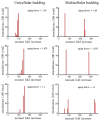
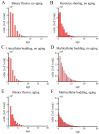
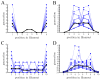
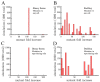
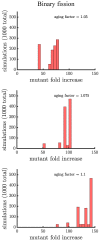
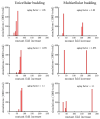
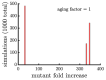
Early multicellular organisms must gain adaptations to outcompete their unicellular ancestors, as well as other multicellular lineages. The tempo and mode of multicellular adaptation is influenced by many factors including the traits of individual cells. We consider how a fundamental aspect of cells, whether they reproduce via binary fission or budding, can affect the rate of adaptation in primitive multicellularity. We use mathematical models to study the spread of beneficial, growth rate mutations in unicellular populations and populations of multicellular filaments reproducing via binary fission or budding. Comparing populations once they reach carrying capacity, we find that the spread of mutations in multicellular budding populations is qualitatively distinct from the other populations and in general slower. Since budding and binary fission distribute age-accumulated damage differently, we consider the effects of cellular senescence. When growth rate decreases with cell age, we find that beneficial mutations can spread significantly faster in a multicellular budding population than its corresponding unicellular population or a population reproducing via binary fission. Our results demonstrate that basic aspects of the cell cycle can give rise to different rates of adaptation in multicellular organisms.
Keywords: adaptation; aging; binary fission; budding; filaments; multicellularity.
Conflict of interest statement
The authors declare no conflict of interest.
Figures


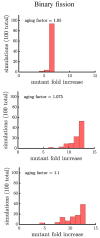

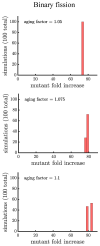
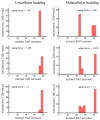
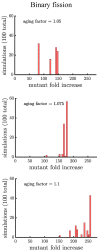

References
-
- Maynard Smith J., Szathmary E. The Major Transitions in Evolution. Oxford University Press; New York, NY, USA: 1997.
-
- Grosberg R.K., Strathmann R.R. The evolution of multicellularity: A minor major transition? Annu. Rev. Ecol. Evol. Syst. 2007;38:621–654. doi: 10.1146/annurev.ecolsys.36.102403.114735. - DOI
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

