Generative Models for Active Vision

Abstract

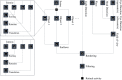
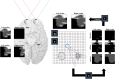
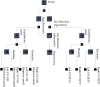
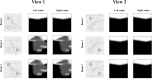
The active visual system comprises the visual cortices, cerebral attention networks, and oculomotor system. While fascinating in its own right, it is also an important model for sensorimotor networks in general. A prominent approach to studying this system is active inference-which assumes the brain makes use of an internal (generative) model to predict proprioceptive and visual input. This approach treats action as ensuring sensations conform to predictions (i.e., by moving the eyes) and posits that visual percepts are the consequence of updating predictions to conform to sensations. Under active inference, the challenge is to identify the form of the generative model that makes these predictions-and thus directs behavior. In this paper, we provide an overview of the generative models that the brain must employ to engage in active vision. This means specifying the processes that explain retinal cell activity and proprioceptive information from oculomotor muscle fibers. In addition to the mechanics of the eyes and retina, these processes include our choices about where to move our eyes. These decisions rest upon beliefs about salient locations, or the potential for information gain and belief-updating. A key theme of this paper is the relationship between "looking" and "seeing" under the brain's implicit generative model of the visual world.

Keywords: Bayesian; active vision; attention; generative model; inference; oculomotion.

Figure 1

A generative model for seeing. This figure offers a summary of a model that generates a retinal image. Starting from the scene in which we find ourselves, we can predict the objects we expect to encounter. These objects may be recursively defined, through identifying their constituent parts and performing a series of geometric (affine) transformations that result in the configuration of parts, the scaling and rotation of this overall configuration, and the placement of these objects in an allocentric reference frame. The nested parts of the graphical structure (on left hand side) indicate this recursive aspect, e.g., an object is defined by an identity, and scaling, rotation and translation parameters; furthermore, it may be composed of various sub-objects each of which has these attributes. To render a retinal image, we also need to know where the retina is and which way it is pointing (i.e., the line of sight available to it). This depends upon where we are in the environment, our heading direction, and where we choose to look. Subsequent figures unpack the parts of this model in greater detail.

Figure 2

The “what” pathway. This figure focuses upon part of the factor graph in Figure 1. In the upper right, this factor graph is reproduced as it might be implemented neuroanatomically. Here, the factors are arranged along the occipitotemporal “what” pathway, which loosely follows those cortical areas superficial to a white matter tract called the inferior longitudinal fasciculus. The panels on the left show the sequence of steps implemented by these factors. Factor a is the distribution over alternative rooms (or scenes) we could find ourselves in. This implies a categorical distribution assigning a probability to each of the rooms provided in the example graphics. Conditioned upon being in a room, we may be able to predict which objects are present. Two example objects are shown (from three orthogonal views). The conditional probability distribution for the geometry of the objects given the room is given by the m factor, which is here broken down into several constituent factors. First, we need to know the identity of the objects in the room (f), which we operationalise in terms of the configuration of the parts of that object. Specifically, we decompose f into a series of transformations (k-l) applied to a set of spheres, which represent the constituents of the object. In principle, we could have used other objects in place of spheres, or could have applied this procedure recursively, such that the constituents of an object can themselves be decomposed into their constituents. Once we have our object, we can apply the same transformations (k-l) to the whole to position it our room. We do this for each object in the room, eventually coming to a representation of all the surfaces in the scene (r), shown in the lower right panel.

Figure 3

The “where” pathway. This figure shows the factors that conspire to generate a field of view. This shows how the allocentric head and egocentric eye-directions (factors d and e) can be combined to compute an allocentric eye-direction (factor p). When this vector is placed so that it originates from the place (factor c) we find ourselves in, we have our field of view (factor q). The graphic in the lower part of this figure maps the associated factors onto the brain structures thought to be involved in representing these variables. The frontal eye-fields (factor e) and the retrosplenial cortex (factor d), both project to the parietal cortex (factor p), which includes regions sensitive to allocentric eye-directions. This communicates with temporoparietal regions (factor q), which are also accessible to hippocampal outputs (factor c) via a pathway comprising the fornix, mammillothalamic, and cingular white matter tracts.

Figure 4

The retinocortical pathway. This figure takes the results from Figures 2, 3 and combines these to arrive at images in each retina. From factors r and q we have our field of view and the surfaces it captures. We can then project from each retinal cell (shown as pixels in the retinal images) to see whether any surface is encountered. For the first surface we reach, we combine the ambient, diffuse, and specular lighting components (factor s). This depends upon factor b from Figure 1, which provides a lighting direction. Once we have the sum of these lighting components, we apply a blurring (factor t) to the image to compensate for the artificial high frequency components introduced by our simplifications. Practically, this is implemented by finding the coefficients of a 2-dimensional discrete cosine transform, multiplying this by a Gaussian function centered on the low frequency coefficients, and then performing the inverse transform. Note that the final image is inverted across the horizontal and vertical planes. This is due to the light reflecting off surfaces on the temporal visual fields being propagated to the retina on the nasal side, and vice versa (with the same inversion in the superior and inferior axis). The fact that the same surface can cause activation of both the right and left retina implies a divergence in the predictions made by parts of the brain dealing in surfaces (e.g., striate cortices) about retinal input. The graphic on the left illustrates the two sorts of visual field defect resulting from this divergence—either interrupting the influence of any surface on one retina (upper image) or interrupting the influence of a subset (e.g., the right half) of all surfaces on either retina (lower image).

Figure 5

A generative model for looking. This figure builds upon part of the model shown in Figure 1. Specifically, it unpacks some of the other sources of data resulting from the eye and head-direction factors and includes a policy variable that determines priors over these variables. These depend upon dynamical systems. This means predicting an equilibrium point (or attractor) that the eyes or head are drawn toward. These dynamics may be divided into changes in the elevation or heading angles. For head movements, the velocity of the head causes changes in the semi-circular canals in the inner ear, communicated to the brain by cranial nerve (CN) VIII. For eye movements, the position and velocity of the eyes give rise to proprioceptive signals due to stretch of the oculomotor muscle tendons, communicated to the brain by CN III, IV, and VI.

Figure 6

Oculomotion. The plots on the left of this figure show an example of the kinds of dynamics that result from Equations (9–12). These illustrate a single saccade toward some equilibrium point determined by factor v. The first two plots detail the hidden states, comprising the heading angle of the eyes, their elevation, and the rates of change of each of these. In addition, the third plot illustrates the proprioceptive data we might expect these dynamics to generate. These are divided into sensory neurons that report instantaneous muscle tendon stretch (II afferents) and those that report changes in this (Ia afferents) for the right and left eye. Note that these differ only in the heading angle—as eye movements are congruent. The constant discrepancy in the heading angle results from the angle of convergence of the eyes. On the right, the factors are arranged to be consistent with the brainstem structures that deal with saccades in the vertical (factor z) and horizontal (factor y) directions. The proprioceptive signal is expressed in arbitrary units (a.u.) which could be converted to firing rates with the appropriate (e.g., sigmoidal) transforms.

Figure 7

Expected information gain. This figure highlights the role of predictive entropies in adjudicating between salient actions. This shows two alternative fields of view we could choose between, through making eye or head movements. If we were not sure which room we were in, view 1 (toward the southeast corner) would be associated with a high predictive entropy, and is consequently useful in resolving uncertainty. In contrast, view 2 (toward the northeast corner) has zero predictive entropy, and does not help distinguish between rooms.