Quantifying the concentration dependence of sedimentation coefficients for globular macromolecules: a continuing age-old problem

Abstract

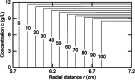
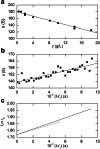
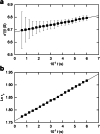
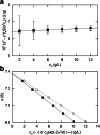
This retrospective investigation has established that the early theoretical attempts to directly incorporate the consequences of radial dilution into expressions for variation of the sedimentation coefficient as a function of the loading concentration in sedimentation velocity experiments require concentration distributions exhibiting far greater precision than that achieved by the optical systems of past and current analytical ultracentrifuges. In terms of current methods of sedimentation coefficient measurement, until such improvement is made, the simplest procedure for quantifying linear s-c dependence (or linear concentration dependence of 1/s) for dilute systems therefore entails consideration of the sedimentation coefficient obtained by standard c(s), g*(s) or G(s) analysis) as an average parameter ( $\overline{s}$ ) that pertains to the corresponding mean plateau concentration (following radial dilution) ( $\overline{c}$ ) over the range of sedimentation velocity distributions used for the determination of $\overline{s}$ . The relation of this with current descriptions of the concentration dependence of the sedimentation and translational diffusion coefficients is considered, together with a suggestion for the necessary improvement in the optical system.

Keywords: Concentration dependence; Optical registration; Sedimentation coefficient; Sedimentation velocity; Ultracentrifugation.

Fig. 1

Effect of radial dilution on the plateau concentration in simulated asymptotic (diffusion-free) sedimentation velocity distributions for a 12-g/L solution of equine γ-globulin (s^o = 7.38 S, k = 0.00785 L/g) subjected to centrifugation at 60,000 rpm for the indicated times (min)

Fig. 2

Early sedimentation velocity studies of tobacco mosaic virus. (a) Graphical representation of the concentration dependence of the sedimentation coefficient reported in Table I of Lauffer (1944). (b) Time-dependence of the measured sedimentation coefficient as the result of radial dilution, the data being taken from Table II of Lauffer (1944). (c) Corresponding time-dependence of the logarithm of boundary position that is predicted by the best-fit linear description of the data in (b): the limiting tangent (broken line) is included to highlight the curvilinearity of the predicted dependence

Fig. 3

Calculated sedimentation velocity behaviour of a protein with the ultracentrifugal characteristics of equine γ-globulin (s^o = 7.38 S, k = 0.00785 L/g). (a) Time-dependence of the sedimentation coefficient s(t) predicted by Eq. (5) from the corresponding boundary positions in Fig. 1. (b) Corresponding time-dependence of the logarithm of the boundary position, which is essentially linear despite the progressive increase in s^∗(t)

Fig. 4

Application of the Baldwin approach to quantifying s^o and k_s for a protein with the sedimentation velocity characteristics of equine γ-globulin. (a) Analysis of the concentration dependence of s(t) data (■) according to Eq. (8) with the fixed time of centrifugation (t_f) set at 6000 s, as well as the corresponding analysis (□) with the mean sedimentation coefficient ($\overline{s}$) substituted for s^∗(t_f). Error bars signify the consequences of an uncertainty of 0.001 cm in r_m and r_b. (b) Dependence of the mean sedimentation coefficient $\overline{s}$ upon concentration defined in terms of loading concentration c_o (□) and the plateau concentration at time $\overline{t}$, the mean of those for first and last sedimentation velocity distributions used to delineate $\overline{s}\left(■\right)$

Fig. 5

Illustration of the g*(s) procedure for determination of the sedimentation coefficient of a monoclonal antibody (IgG) to diphtheria toxin. [Data taken from Fig. 4 of Stafford 1992]

Fig. 6

Evaluation of a sedimentation coefficient by the Van Holde-Weischet procedure. (a) Boundary analysis of sedimentation distributions (48,000 rpm) for fragment K of PM2 DNA in accordance with Eq. (11) to obtain s by the extrapolation of apparent sedimentations coefficients to infinite time. (b) Illustration of solute homogeneity by means of the asymptotic G(s) distribution derived therefrom. [Data in (a) has been taken from Fig. 4 of Van Holde and Weischet 1978]

Fig. 7

Evaluation of the sedimentation coefficient of a laminin short-arm fragment (0.6 g/L) in Tris-chloride buffer (pH 8.5, I 0.17) by c(s) analysis of absorbance distributions resulting from centrifugation at 35,000 rpm. [Data taken from Fig. 5C of Patel et al. (2016)]

Fig. 8

Quantification of the s-c dependence for bovine serum albumin in phosphate-buffered saline by plotting the sedimentation coefficient,${\overline{s}}_{20.w}$, obtained by the standard SEDFIT analysis of sedimentation velocity distributions as a function of the corresponding mean plateau concentration, $\overline{c}$ . Values of s^o_20,w = (4.38± 0.02)S and k_s = (0.0072 ± 0.0003) L/g are returned

Fig. 9

Allowance for concentration dependence of the sedimentation coefficient in the analysis of sedimentation velocity distributions for a reference monoclonal antibody (SRM 8671, NIST, Gaithersburg) centrifuged at 45,000 rpm in 25mM histidine buffer. The solid line describes the (monomer) distribution obtained by the refined c_NI(s_o) analysis, whereas the broken line is the corresponding distribution obtained by the standard c(s) procedure. A dimer peak compromising 2.7% of the material present is not shown. [Data taken with permission from Fig. 2 of Chaturvedi et al. 2018]

Fig. 10

Concentration dependence of the translational diffusion coefficient for bovine serum albumin. Comparison of results [Table 4 of Creeth 1952)] obtained under various solvent conditions by the traditional boundary spreading procedure with theoretically predicted concentration dependences. The combined data are fitted to Batchelor-Felderhof and Brady-Durlofsky representations (with and without allowance for solution viscosity)