Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2021 Apr 30;23(5):560.
doi: 10.3390/e23050560.

Entropy Based Student's t-Process Dynamical Model

Ayumu Nono  1 , Yusuke Uchiyama  2 , Kei Nakagawa  3
Affiliations

Entropy Based Student's t-Process Dynamical Model

Ayumu Nono et al. Entropy (Basel). .

Abstract

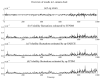
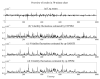
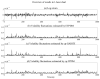
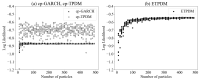
Volatility, which represents the magnitude of fluctuating asset prices or returns, is used in the problems of finance to design optimal asset allocations and to calculate the price of derivatives. Since volatility is unobservable, it is identified and estimated by latent variable models known as volatility fluctuation models. Almost all conventional volatility fluctuation models are linear time-series models and thus are difficult to capture nonlinear and/or non-Gaussian properties of volatility dynamics. In this study, we propose an entropy based Student's t-process Dynamical model (ETPDM) as a volatility fluctuation model combined with both nonlinear dynamics and non-Gaussian noise. The ETPDM estimates its latent variables and intrinsic parameters by a robust particle filtering based on a generalized H-theorem for a relative entropy. To test the performance of the ETPDM, we implement numerical experiments for financial time-series and confirm the robustness for a small number of particles by comparing with the conventional particle filtering.

Keywords: Student’s t-process; entropy based particle filter; finance; relative entropy; volatility fluctuation.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Overview of estimation results in 1-min chart.
Figure 2
Figure 2
Overview of estimation results in 30-min chart.
Figure 3
Figure 3
Overview of estimation results in 1-h chart.
Figure 4
Figure 4
Estimated log-likelihoods of (a) the cp-GARCH, the cp-TPDM and (b) the ETPDM.
Figure 5
Figure 5
Effective particle rates of (a) cp-GARCH, the cp-TPDM and (b) the ETPDM.
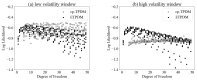
Figure 6
Figure 6
Log-likelihoods of the cp-TPDM and the ETPDM in (a) low volatility window and (b) high volatility one.
See this image and copyright information in PMC

References

    1. Cochrane J.H. Asset Pricing: Revised Edition. Princeton University Press; Princeton, NJ, USA: 2009.
    1. Mandelbrot B.B. Fractals and Scaling in Finance. Springer; Berlin/Heidelberg, Germany: 1997. The variation of certain speculative prices; pp. 371–418.
    1. Shang Y., Dong Q. Applied Economics. Routledge; London, UK: 2021. Oil volatility forecasting and risk allocation: Evidence from an extended mixed-frequency volatility model; pp. 1127–1142.
    1. Hou Y., Li S., Wen F. Time-varying volatility spillover between Chinese fuel oil and stock index futures markets based on a DCC-GARCH model with a semi-nonparametric approach. Energy Econ. 2019;83:119–143. doi: 10.1016/j.eneco.2019.06.020. - DOI
    1. Horvath B., Muguruza A., Tomas M. Deep Learning Volatility. arXiv. 2019 doi: 10.2139/ssrn.3322085.1901.09647 - DOI

LinkOut - more resources