AI-assisted superresolution cosmological simulations

Abstract

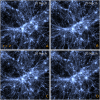
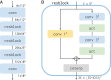
Cosmological simulations of galaxy formation are limited by finite computational resources. We draw from the ongoing rapid advances in artificial intelligence (AI; specifically deep learning) to address this problem. Neural networks have been developed to learn from high-resolution (HR) image data and then make accurate superresolution (SR) versions of different low-resolution (LR) images. We apply such techniques to LR cosmological N-body simulations, generating SR versions. Specifically, we are able to enhance the simulation resolution by generating 512 times more particles and predicting their displacements from the initial positions. Therefore, our results can be viewed as simulation realizations themselves, rather than projections, e.g., to their density fields. Furthermore, the generation process is stochastic, enabling us to sample the small-scale modes conditioning on the large-scale environment. Our model learns from only 16 pairs of small-volume LR-HR simulations and is then able to generate SR simulations that successfully reproduce the HR matter power spectrum to percent level up to [Formula: see text] and the HR halo mass function to within [Formula: see text] down to [Formula: see text] We successfully deploy the model in a box 1,000 times larger than the training simulation box, showing that high-resolution mock surveys can be generated rapidly. We conclude that AI assistance has the potential to revolutionize modeling of small-scale galaxy-formation physics in large cosmological volumes.

Keywords: cosmology; deep learning; simulation; super resolution.

Fig. 1.

Two-dimensional projections of the LR, HR, and SR dark-matter density fields at $z=0$. The blue background shows the smoothed density field of all of the dark-matter particles. The particles in FOF groups are highlighted in orange to help visually identify the halos. The top images show slabs from the full box of 100 $h^{-1}\mathrm{\text{Mpc}}$ side length and 20 $h^{-1}\mathrm{\text{Mpc}}$ thickness. The middle images zoom into the orange boxes (A) from the top image, each of size ${\left(20\hspace{0.17em}{h}^{-1}\mathrm{\text{Mpc}}\right)}^3$. The bottom two rows show the four zoom-in boxes (B–E), which are ${\left(10\hspace{0.17em}{h}^{-1}\mathrm{\text{Mpc}}\right)}^3$ in size, to reveal even finer details. The first two columns show the LR and HR simulations, which have the same initial conditions, but a factor of $512\times$ different mass resolution. The rightmost column shows one of the SR realizations generated by our trained model. All density projections are smoothed by a Gaussian filter on a scale of 5 $h^{-1}\hspace{0.17em}\mathrm{\text{kpc}}$, using gaepsi2 (https://github.com/rainwoodman/gaepsi2).

Fig. 2.

Using our GAN-based algorithm, we can generate different SR realizations from the same LR inputs. We show one HR and three random SR projections, of the same ${\left(20\hspace{0.17em}{h}^{-1}\mathrm{\text{Mpc}}\right)}^3$ regions and the same LR field, at $z=2$. To demonstrate their remarkable similarities, we intentionally omit the HR and SR labels in panels A–D and invite the readers to guess which panel is HR before checking the answer in the footnote.* The HR and three SR realizations have the same large-scale structures, but are all different in their small-scale features. Yet, they appear statistically indistinguishable. The color scheme and smoothing method are the same as in Fig. 1.*The answer to Fig. 2 is A.

Fig. 3.

Dimensionless matter power spectrum ${\mathrm{\Delta }}^2$ comparison on LR (purple), HR (blue), and SR (black) test realizations, at $z=\mathrm{4,2}$, and 0. The vertical dashed lines mark the Nyquist wavenumber. LR power quickly vanishes on small scales at $z=4$. This deficit persists and is partly compensated by formation of poorly resolved halos at $z=2$ and $z=0$. The SR result is a dramatic improvement, with the SR power spectra matching the HR curves remarkably well, within a few percent on all scales at all redshifts.

Fig. 4.

FOF halo mass function comparison among LR (purple), HR (blue), and SR (black) test simulations, at $z=\mathrm{4,2}$, and 0. The LR simulations can only resolve the most massive halos ($M_{\mathrm{h}}\gtrsim 10^{13}\hspace{0.17em}{M}_{\odot }$). Our generated SR fields have the same mass resolution as the HR fields, resolving halos all of the way down to $10^{11}\hspace{0.17em}{M}_{\odot }$. Their halo populations closely match the HR results, at the $10\%$ level throughout the mass range.

Fig. 5.

Illustration of the ${\left(1\hspace{0.17em}{h}^{-1}\mathrm{\text{Gpc}}\right)}^3$ volume SR with $5120^3$ particles generated from the input $640^3$ LR field using our GAN model. Colors are the same as in Fig. 1. The large panel shows a slice through the full box, 1 $\hspace{0.17em}{h}^{-1}\mathrm{\text{Gpc}}$ in length and 20 $h^{-1}\mathrm{\text{Mpc}}$ in thickness. The top left inset in the white box shows the same field from the LR simulation. In the two red inset panels, we show a ${\left(20\hspace{0.17em}{h}^{-1}\mathrm{\text{Mpc}}\right)}^3$ zoom-in region around a massive halo in both the SR and LR field. That central halo has a mass of $2\times 10^{14}\hspace{0.17em}{M}_{\odot }$, larger than the most massive halo in the ${\left(100\hspace{0.17em}{h}^{-1}\mathrm{\text{Mpc}}\right)}^3$ volume training set. The generating process only takes about 16 h on one GPU.

Fig. 6.

Halo mass function comparison of the ${\left(1\hspace{0.17em}\hspace{0.17em}{h}^{-1}\mathrm{\text{Gpc}}\right)}^3$ LR (blue), the ${\left(1\hspace{0.17em}\hspace{0.17em}{h}^{-1}\mathrm{\text{Gpc}}\right)}^3$ SR (black and generated from the former), and the ${\left(100\hspace{0.17em}{h}^{-1}\mathrm{\text{Mpc}}\right)}^3$ HR (orange) simulations at $z=2$. Limited by mass resolution, the LR run only resolves the most massive halos with $M_{\mathrm{h}}\gtrsim 10^{13}\hspace{0.17em}{M}_{\odot }$. Also, limited by volume, the HR run lacks halos above $M_{\mathrm{h}}\gtrsim 10^{14}\hspace{0.17em}{M}_{\odot }$. Our SR realization is able to match both the resolved LR and HR abundances over the whole mass range. We emphasize that our model generalizes surprisingly well to successfully predict the mass function of the massive halos that it has not been trained on, for over three orders of magnitude in abundance, demonstrating its extrapolating power in modeling structure formations.

Fig. 7.

Generator network architecture, inspired by StyleGAN2. The whole network structure is shown in A, with components enlarged in B and C. The colored plates are different operations, connected by lines or arrows from the input to the output. The sizes (channel number $\times$ spatial size) of the input, intermediate, and output tensors are next to the arrows. The generator takes the shape of a ladder, where each rung upsamples the data by $2\times$. The left rail consists of consecutive convolution blocks (“conv” in blue plates) operating in the high-dimensional latent space and is projected (“proj” in yellow plates) at every step to the low-dimensional output space on the right rail. The projected results are then upsampled by linear interpolation (“interp” in gray plates), before being summed into the output. A key ingredient is the addition of noise (on red plates), which adds stochasticity absent from the input at each level of resolution. The added noises are then transformed into high-frequency features by the subsequent convolutions and activations. The kernel sizes of the convolutions are labeled in their plates (that distinguish them from the conv block). Note that with a kernel size one, “conv $1^3$” is simply an affine transformation along the channel dimensions, and thus a convolution only in the technical sense. All activation functions (“act” in green plates) are Leaky ReLU with slope 0.2 for negative values. All conv blocks have the same structure as shown in B, except the first one, which starts with an additional $1^3$ convolution and an activation.

Fig. 8.

Discriminator (critic) network architecture, inspired by the StyleGAN2. The whole network structure is shown in A, with the residual block enlarged in B. The residual block consists of two branches: The so-called “skip” branch is only a $1^3$ convolution, and, on top of that, the other branch has real convolutions and activations to learn the “residuals.” It then downsamples by $2\times$ the sum of the two branches with linear interpolation. Aside from the residual blocks, the first conv block includes a $1^3$ convolution followed by an activation, and the last conv block has a $1^3$ convolution to double the channel, an activation, and a $1^3$ convolution to reduce the channel to 1. See Fig. 7 for other details.