A simple criterion to design optimal non-pharmaceutical interventions for mitigating epidemic outbreaks

Abstract

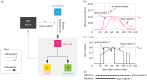
For mitigating the COVID-19 pandemic, much emphasis is made on implementing non-pharmaceutical interventions to keep the reproduction number below one. However, using that objective ignores that some of these interventions, like bans of public events or lockdowns, must be transitory and as short as possible because of their significant economic and societal costs. Here, we derive a simple and mathematically rigorous criterion for designing optimal transitory non-pharmaceutical interventions for mitigating epidemic outbreaks. We find that reducing the reproduction number below one is sufficient but not necessary. Instead, our criterion prescribes the required reduction in the reproduction number according to the desired maximum of disease prevalence and the maximum decrease of disease transmission that the interventions can achieve. We study the implications of our theoretical results for designing non-pharmaceutical interventions in 16 cities and regions during the COVID-19 pandemic. In particular, we estimate the minimal reduction of each region's contact rate necessary to control the epidemic optimally. Our results contribute to establishing a rigorous methodology to design optimal non-pharmaceutical intervention policies for mitigating epidemic outbreaks.

Keywords: COVID-19; epidemic outbreak; non-pharmaceutical interventions; optimal control.

Figure 1.

Optimal non-pharmaceutical interventions. (a) Susceptible–Infected–Removed (SIR) model with non-pharmaceutical interventions (NPIs) reducing disease transmission. For the optimal NPI design problem, the objective is to design the intervention u*(t) with minimal effective duration such that u*(t) ∈ [0, u_max] and I(t) ≤ I_max for all t ≥ 0. (b,c) The response of the SIR model for two interventions (parameters are β = 0.52, γ = 1/7, I₀ = 8.855 × 10⁻⁷ and S₀ = 1 − I₀). Both interventions 1 and 2 satisfy u(t) ≤ u_max and guarantee that I(t) ≤ I_max. Actually, intervention 2 is the optimal one derived using our analysis: it is the intervention with minimal effective duration satisfying I(t) ≤ I_max. (d) The effective duration of an intervention measures the interval between the start of the outbreak and the last time that a non-zero intervention is applied. In this example, the effective duration of intervention 1 is 120 days, while the effective duration of intervention 2 is 69 days.

Figure 2.

Existence of non-pharmaceutical interventions in the Susceptible–Infected–Removed model. Parameters are γ = 1/7, β = 0.52 (i.e. R₀ = 3.64) and I_max = 0.1. The safe zone (in blue) consists of all states that do not exceed I_max without interventions. This zone is characterized by the inequality $I\le {\mathit{\Phi }}_{R_0}(S)$. The plane is further divided into feasible states that can reach the safe zone without exceeding I_max (white), and unfeasible states that cannot (grey). Feasible and unfeasible states are separated by the separating curve ${\mathit{\Phi }}_{R_c}(S)$ (black line). (a) For ‘strong’ interventions with u_max = 0.8, the controlled reproduction number is R_c = (1 − u_max)R₀ = 0.728 < 1. Here, the separating curve is the straight line I_max, implying that all states below I_max are feasible. Note this case corresponds to eradication. (b) For ‘intermediate’ interventions with u_max = 0.6, the controlled reproduction number is R_c = (1 − u_max)R₀ = 1.456 > 1. Here, the separating curve ${\mathit{\Phi }}_{R_c}(S)$ is nonlinear, and some states below I_max are unfeasible. (c) For ‘weak’ interventions with u_max = 0.4 we obtain R_c = 2.184 > 1. In this case, states with S(0) ≈ 1 are unfeasible. (d) For S(0) → 1, our design criterion for NPIs prescribes the values of R_c that a given I_max can manage.

Figure 3.

Optimal non-pharmaceutical interventions in the Susceptible–Infected–Removed model. For all panels, the parameters of the SIR model are γ = 1/7, β = 0.52 (i.e. R₀ = 3.64) and I_max = 0.1. We consider a population of N = 8.855 × 10⁶ individuals (like in Mexico City) and I₀ = 1/N. Panels shows trajectories for three initial proportions of the susceptible population: large S₀ = 1 − I₀ ≈ 1 (pink), medium S₀ = 0.8 (green) and small S₀ = 0.65 (purple). (a) For u_max = 0.8, we have R_c = (1 − u_max)R₀ = 0.728 ≤ 1. In this case, the optimal intervention starts when the disease prevalence reaches I_max. Afterwards, the intervention decreases in a hyperbolic arc until reaching the point S = S*. At that time, the intervention becomes maximum in the ‘final push’ to reach the safe zone. (b) For u_max = 0.58, the controlled reproduction number is R_c = (1 − u_max)R₀ = 1.52 > 1. Here, ${\mathit{\Phi }}_{R_c}(1)>0$, implying that the epidemic still can be mitigated for initial states with S₀ ≈ 1 and I₀ ≈ 0 (pink trajectory). In this case, the optimal intervention starts when the initial condition hits the separating curve below I_max at t = 35. At that instant, the intervention starts with the maximum value u_max, and continues in that form until the trajectory reaches I_max. (c) Choosing u_max = 0.4 yields R_c = 2.184 > 1. In this case, the optimal intervention problem does not have a solution for all initial states S₀ > 0.85. This is illustrated by pink trajectory: even when applying the maximum intervention from the start, I(t) will grow beyond I_max.

Figure 4.

Optimal non-pharmaceutical interventions are robust. For all panels, the estimated parameters used for constructing the optimal NPIs are $\hat{\gamma }=1/7$, $\hat{\beta }=0.52$, I_max = 0.1, u_max = 0.6. We consider a population of N = 8.855 × 10⁶ as in Mexico City, and the initial conditions I(0) = 1/N and S(0) = 1 − 1/N. If the models contain other state variables, they were initialized at zero. The optimal NPIs are constructed assuming ${\hat{R}}_0=\hat{\beta }/\hat{\gamma }$, while the actual epidemic dynamics has a possibly different R₀ = β/γ. Panels show results for outbreaks with three values of R₀: low (yellow), medium (orange) and large (red). (a) SIR model where the reduction in the disease transmission by the NPIs is uncertain. We model this case replacing u by ku in the model equations. Panel shows the results for k = 1.1 (dotted), k = 1 (solid) and k = 0.9 (dashed). (b) SEIR model where exposed individuals do not transmit the infection, with λ > 0 the incubation period. Panel shows the results for λ = 1/5 (dotted), λ = 1/7 (solid) and λ = 1/11 (dashed). (c) SEIIR model with λ = 1/7 and two classes of infected individuals (symptomatic and asymptomatic). Here, p ∈ [0, 1] is the proportion of exposed individuals that become asymptomatic. The vertical axis denotes the disease prevalence for symptomatic individuals. The panel shows the results for p = 0.55 (dotted), p = 0.7 (solid) and p = 0.8 (dashed).

Figure 5.

Minimum necessary reduction in disease transmission for NPIs in the COVID-19 pandemic. (a) Calculated I_max according to the proportion of available intensive care beds in each region or city and the estimated fraction of infected individuals requiring intensive care. (b) Maximum controlled reproduction number R_c that each region or city can handle according to its I_max. Larger I_max allows a larger R_c. (c) Basic reproduction number R₀ per region or city before interventions started. Median (blue big dot), and 95% confidence interval (smaller dots) are shown. (d) Minimum u_max necessary for feasibility for each region or city (blue) according to the R₀ of (c). Grey bars denote the reported average mobility reduction in each region between 19 March and 30 April 2020.