Power of data in quantum machine learning

Abstract

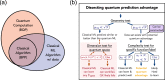
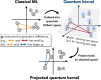
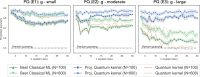
The use of quantum computing for machine learning is among the most exciting prospective applications of quantum technologies. However, machine learning tasks where data is provided can be considerably different than commonly studied computational tasks. In this work, we show that some problems that are classically hard to compute can be easily predicted by classical machines learning from data. Using rigorous prediction error bounds as a foundation, we develop a methodology for assessing potential quantum advantage in learning tasks. The bounds are tight asymptotically and empirically predictive for a wide range of learning models. These constructions explain numerical results showing that with the help of data, classical machine learning models can be competitive with quantum models even if they are tailored to quantum problems. We then propose a projected quantum model that provides a simple and rigorous quantum speed-up for a learning problem in the fault-tolerant regime. For near-term implementations, we demonstrate a significant prediction advantage over some classical models on engineered data sets designed to demonstrate a maximal quantum advantage in one of the largest numerical tests for gate-based quantum machine learning to date, up to 30 qubits.

Fig. 1. Illustration of the relation between complexity classes and a flowchart for understanding and prescreening potential quantum advantage.

a We cartoon the separation between problem complexities that are created by the addition of data to a problem. Classical algorithms that can learn from data define a complexity class that can solve problems beyond classical computation (BPP), but it is still expected that quantum computation can efficiently solve problems that classical ML algorithms with data cannot. A rigorous definition and proof for the separation between classical algorithms that can learn from data and BPP/BQP is given in Supplementary Section 2. b The flowchart we develop for understanding the potential for quantum prediction advantage. N samples of data from a potentially infinite depth QNN made with encoding and function circuits U_enc and U_QNN are provided as input along with quantum and classical methods with associated kernels. Tests are given as functions of N to emphasize the role of data in the possibility of a prediction advantage. One can first evaluate a geometric quantity g_CQ that measures the possibility of an advantageous quantum/classical prediction separation without yet considering the actual function to learn. We show how one can efficiently construct an adversarial function that saturates this limit if the test is passed, otherwise the classical approach is guaranteed to match performance for any function of the data. To subsequently consider the actual function provided, a label/function-specific test may be run using the model complexities s_C and s_Q. If one specifically uses the quantum kernel (QK) method, the red dashed arrows can evaluate if all possible choices of U_QNN lead to an easy classical function for the chosen encoding of the data.

Fig. 2. Cartoon of the geometry (kernel function) defined by classical and quantum ML models.

The letters A, B, ... represent data points {x_i} in different spaces with arrows representing the similarity measure (kernel function) between data. The geometric difference g is a difference between similarity measures (arrows) in different ML models and d is an effective dimension of the dataset in the quantum Hilbert space.

Fig. 3. Relation between dimension d, geometric difference g, and prediction performance.

The shaded regions are the standard deviation over 10 independent runs and n is the number of qubits in the quantum encoding and dimension of the input for the classical encoding. a The approximate dimension d and the geometric difference g with classical ML models for quantum kernel (Q) and projected quantum kernel (PQ) under different embeddings and system sizes n. b Prediction error (lower is better) of the quantum kernel method (Q), projected quantum kernel method (PQ), and classical ML models on classical (C) and quantum (Q) datasets with number of data N = 600. As d grows too large, the geometric difference g for quantum kernel becomes small. We see that small geometric difference g always results in classical ML being competitive or outperforming the quantum ML model. When g is large, there is a potential for improvement over classical ML. For example, projected quantum kernel improves upon the best classical ML in Dataset (Q, E3).

Fig. 4. Prediction accuracy (higher the better) on engineered datasets.

A label function is engineered to match the geometric difference g(C∣∣PQ) between projected quantum kernel and classical approaches, demonstrating a significant gap between quantum and the best classical models up to 30 qubits when g is large. We consider the best performing classical ML models among Gaussian SVM, linear SVM, Adaboost, random forest, neural networks, and gradient boosting. We only report the accuracy of the quantum kernel method up to system size n = 28 due to the high simulation cost and the inferior performance.