Fast computational mutation-response scanning of proteins
- PMID: 33976988
- PMCID: PMC8067912
- DOI: 10.7717/peerj.11330
Fast computational mutation-response scanning of proteins
Abstract
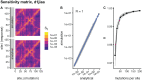
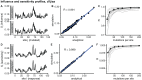
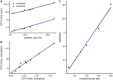
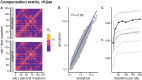
Studying the effect of perturbations on protein structure is a basic approach in protein research. Important problems, such as predicting pathological mutations and understanding patterns of structural evolution, have been addressed by computational simulations that model mutations using forces and predict the resulting deformations. In single mutation-response scanning simulations, a sensitivity matrix is obtained by averaging deformations over point mutations. In double mutation-response scanning simulations, a compensation matrix is obtained by minimizing deformations over pairs of mutations. These very useful simulation-based methods may be too slow to deal with large proteins, protein complexes, or large protein databases. To address this issue, I derived analytical closed formulas to calculate the sensitivity and compensation matrices directly, without simulations. Here, I present these derivations and show that the resulting analytical methods are much faster than their simulation counterparts.
Keywords: Compensatory mutations; Mutational response; Protein.
© 2021 Echave.
Conflict of interest statement
The author declares that he has no competing interests.
Figures
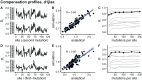
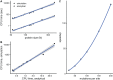
Similar articles
-
Intragenic compensation through the lens of deep mutational scanning.Biophys Rev. 2022 Oct 26;14(5):1161-1182. doi: 10.1007/s12551-022-01005-w. eCollection 2022 Oct. Biophys Rev. 2022. PMID: 36345285 Free PMC article. Review.
-
Characterization of compensated mutations in terms of structural and physico-chemical properties.J Mol Biol. 2007 Jan 5;365(1):249-56. doi: 10.1016/j.jmb.2006.09.053. Epub 2006 Sep 26. J Mol Biol. 2007. PMID: 17059831
-
Effects of point mutation on enzymatic activity: correlation between protein electronic structure and motion in chorismate mutase reaction.J Am Chem Soc. 2010 May 26;132(20):7104-18. doi: 10.1021/ja100744h. J Am Chem Soc. 2010. PMID: 20426479
-
Predicting binding affinity changes from long-distance mutations using molecular dynamics simulations and Rosetta.Proteins. 2023 Jul;91(7):920-932. doi: 10.1002/prot.26477. Epub 2023 Mar 2. Proteins. 2023. PMID: 36757060
-
Learning Strategies in Protein Directed Evolution.Methods Mol Biol. 2022;2461:225-275. doi: 10.1007/978-1-0716-2152-3_15. Methods Mol Biol. 2022. PMID: 35727454 Review.
References
-
- Echave J. Evolutionary divergence of protein structure: the linearly forced elastic network model. Chemical Physics Letters. 2008;457(4–6):413–416. doi: 10.1016/j.cplett.2008.04.042. - DOI
LinkOut - more resources
Full Text Sources
Other Literature Sources

