Mathematical modeling of the COVID-19 pandemic with intervention strategies
- PMID: 33977079
- PMCID: PMC8101006
- DOI: 10.1016/j.rinp.2021.104285
Mathematical modeling of the COVID-19 pandemic with intervention strategies
Abstract
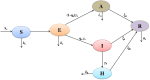
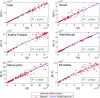
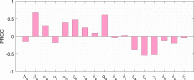
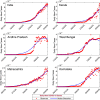
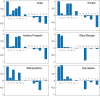
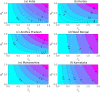
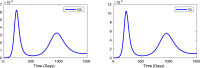
Mathematical modeling plays an important role to better understand the disease dynamics and designing strategies to manage quickly spreading infectious diseases in lack of an effective vaccine or specific antivirals. During this period, forecasting is of utmost priority for health care planning and to combat COVID-19 pandemic. In this study, we proposed and extended classical SEIR compartment model refined by contact tracing and hospitalization strategies to explain the COVID-19 outbreak. We calibrated our model with daily COVID-19 data for the five provinces of India namely, Kerala, Karnataka, Andhra Pradesh, Maharashtra, West Bengal and the overall India. To identify the most effective parameters we conduct a sensitivity analysis by using the partial rank correlation coefficients techniques. The value of those sensitive parameters were estimated from the observed data by least square method. We performed sensitivity analysis for to investigate the relative importance of the system parameters. Also, we computed the sensitivity indices for to determine the robustness of the model predictions to parameter values. Our study demonstrates that a critically important strategy can be achieved by reducing the disease transmission coefficient and clinical outbreak rate to control the COVID-19 outbreaks. Performed short-term predictions for the daily and cumulative confirmed cases of COVID-19 outbreak for all the five provinces of India and the overall India exhibited the steady exponential growth of some states and other states showing decays of daily new cases. Long-term predictions for the Republic of India reveals that the COVID-19 cases will exhibit oscillatory dynamics. Our research thus leaves the option open that COVID-19 might become a seasonal disease. Our model simulation demonstrates that the COVID-19 cases across India at the end of September 2020 obey a power law.
Keywords: Basic reproduction number; India; Model prediction; Power law; Sensitivity analysis.
© 2021 The Authors.
Conflict of interest statement
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Figures
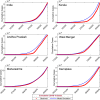
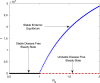
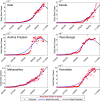
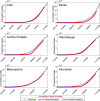
References
-
- 2020. Coronavirus disease (COVID-19) outbreak situation.https://www.who.int/emergencies/diseases/novel-coronavirus -2019.
-
- Cohen J., Normile D. New SARS-like virus in China triggers alarm. Science. 2020;367:234–235. - PubMed
LinkOut - more resources
Full Text Sources
Other Literature Sources
