Cellular connectomes as arbiters of local circuit models in the cerebral cortex
- PMID: 33986261
- PMCID: PMC8119988
- DOI: 10.1038/s41467-021-22856-z
Cellular connectomes as arbiters of local circuit models in the cerebral cortex
Abstract
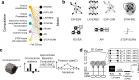
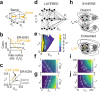
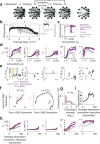
With the availability of cellular-resolution connectivity maps, connectomes, from the mammalian nervous system, it is in question how informative such massive connectomic data can be for the distinction of local circuit models in the mammalian cerebral cortex. Here, we investigated whether cellular-resolution connectomic data can in principle allow model discrimination for local circuit modules in layer 4 of mouse primary somatosensory cortex. We used approximate Bayesian model selection based on a set of simple connectome statistics to compute the posterior probability over proposed models given a to-be-measured connectome. We find that the distinction of the investigated local cortical models is faithfully possible based on purely structural connectomic data with an accuracy of more than 90%, and that such distinction is stable against substantial errors in the connectome measurement. Furthermore, mapping a fraction of only 10% of the local connectome is sufficient for connectome-based model distinction under realistic experimental constraints. Together, these results show for a concrete local circuit example that connectomic data allows model selection in the cerebral cortex and define the experimental strategy for obtaining such connectomic data.
Conflict of interest statement
The authors declare no competing interests
Figures



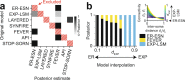
References
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

