Beyond Euler/Cardan analysis: True glenohumeral axial rotation during arm elevation and rotation

Abstract

Background: Based on Euler/Cardan analysis, prior investigations have reported up to 80° of glenohumeral (GH) external rotation during arm elevation, dependent on the plane of elevation (PoE). However, the subtraction of Euler/Cardan angles does not compute the rotation around the humerus' longitudinal axis (i.e. axial rotation). Clinicians want to understand the true rotation around the humerus' longitudinal axis and rely on laboratories to inform their understanding of underlying shoulder biomechanics, especially for the GH joint since its motion cannot be visually ascertained. True GH axial rotation has not been previously measured in vivo, and its difference from Euler/Cardan (apparent) axial rotation is unknown.

Research question: What is the true GH axial rotation during arm elevation and external rotation, and does it vary from apparent axial rotation and by PoE?

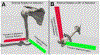
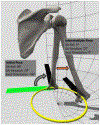
Methods: Twenty healthy subjects (10 M/10 F, ages 22-66) were recorded using biplane fluoroscopy while performing arm elevation in the coronal, scapular and sagittal planes, and external rotation in 0° and 90° of abduction. Apparent GH axial rotation was computed using the xz'y'' and yx'y'' sequences. True GH axial rotation was computed by integrating the projection of GH angular velocity onto the humerus' longitudinal axis. One-dimensional statistical parametric mapping was utilized to compare apparent versus true axial rotation, axial rotation versus 0°, and detect differences in axial rotation by PoE.

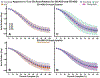
Results: In contrast to apparent axial rotation, true GH axial rotation does not differ by PoE and is not different than 0° during arm elevation at higher elevation angles. The spherical area between the sequence-specific and actual humeral trajectory explains the difference between apparent and true axial rotation.

Significance: Proper quantification of axial rotation is important because biomechanics literature informs clinical understanding of shoulder biomechanics. Clinicians care about true axial rotation, which should be reported in future studies of shoulder kinematics.

Keywords: Biplane fluoroscopy; Glenohumeral; Kinematic analysis; True axial rotation.

Fig. 1:

Graphical depiction of external rotation in the transverse plane (A, External Rotation in Adduction, ER-ADD) and external rotation in the sagittal plane (B, External Rotation at 90° of Abduction, ER-ABD). For ER-ADD trials, subjects were instructed to maintain the elbow by their torso with the hand on the abdomen and thumb pointing up, and to laterally rotate to their full ROM at ~45°/sec. For ER-ABD trials, subjects were instructed to point their elbow towards the side of the room while allowing the hand to hang naturally due to its weight, and laterally rotate up to their full ROM at ~45°/sec. Green lines denote the starting position of the forearm axis, and red lines denote the ending position of the forearm axis.

Fig. 2:

Spherical area illustrations for arm elevation motions. The xz’y” (A) and the yx’y” (B) decompositions yield the sequence-specific humeral trajectory (brown), where the actual humeral trajectory (blue) is shown for coronal plane abduction (left), scapular plane abduction (middle), and forward elevation (right). Apparent GH axial rotation is computed by following the sequence-specific humeral trajectory, while true GH axial rotation is computed by following the actual humeral trajectory. The spherical area encompassed between the two trajectories represents the absolute value of the difference between apparent and true axial rotation. Appendix 1 details how the paths were constructed. The position of the distal humerus on the sphere at 30°, 90°, and 120° of HT elevation is indicated on the sphere to demonstrate how the spherical area changes with increased HT elevation angles.

Fig. 3:

Comparison between the coronal, scapular, and sagittal planes of elevation for true (D), xz’y” (E), yx’y” (F), and swing-spin (G) GH axial rotation. The left column portrays the axial orientation plots for xz’y” (A), yx’y” (B), and swing-spin (C) from which apparent axial rotation was derived. The singular data points indicate axial orientation/rotation at minimum/maximum HT elevation (differs by subject). The errors bars around the singular data point and the shaded regions indicate ±1 standard deviation. The black solid line at the top of plots on the right column indicates regions where a SPM1D one-way repeated-measures ANOVA test found a difference in axial rotation between planes of elevation (CA, SA, FE) – a suprathreshold event. The following suprathreshold events exceeded p≤0.001: swing-spin between 25°-78° of HT elevation (p=0.006), and beyond 128° of HT elevation (p=0.050). The colored solid lines (green for CA, purple for SA, and orange for FE) at the top of plots on the right column indicate regions where a SPM1D non-parametric t-test found significant differences from 0° of axial rotation. The following suprathreshold events exceeded p≤0.001: true axial rotation for SA (p=0.002), xz’y” for SA between 122°-130° of HT elevation (p=0.02), swing-spin for FE (p=0.002).

Fig. 4:

Comparison of xz’y” (A-C), yx’y”, and swing-spin (D-F) apparent GH axial rotation versus true GH axial rotation for CA (A, D), SA (B, E), and FE (C, F). The singular data point indicates axial rotation at maximum HT elevation (differs by subject). The errors bars around the singular data point and the shaded regions indicate ±1 standard deviation. The solid lines (orange for xz’y”, green for yx’y”, and magenta for swing-spin) at the top of each plot indicate regions where a SPM1D non-parametric paired t-test found significant differences between apparent and true axial rotation. The following suprathreshold events exceeded p≤0.001: xz’y” for SA between 25°-29° of HT elevation (p=0.020), and between 91°-130° of HT elevation (p=0.003).

Fig. 5:

Comparison of xz’y” (A, B), yx’y”, and swing-spin (C, D) GH apparent axial rotation versus true GH axial rotation for ER-ADD (A, C) and ER-ABD (B, D). Trials were interpolated at 0.25% increments between the start (0%) of the motion and maximum external rotation (100%). The shaded regions indicate ±1 standard deviation. The solid lines (orange for xz’y”, green for yx’y”, and magenta for swing-spin) at the top of each plot indicate regions where a SPM1D non-parametric paired t-test found significant differences between apparent and true axial rotation. The following suprathreshold events exceeded p≤0.001: xz’y” for ER-ABD beyond 70% of motion completion (p=0.002).

Fig. 6:

Illustration of how changes in PoE affect axial rotation as measured by the yx’y” sequence during CA, with the forearm (black rectangle) pointing anteriorly. Because of body habitus and posture, in the initial pose the humerus is slightly elevated (20°) in the sagittal plane. Since for the yx’y” sequence axial orientation is measured from an axis (green) that is tangent to the latitude (yellow circle), one would measure 90° of external axial orientation. As the subject elevates in the coronal plane, with the forearm still pointing anteriorly, they arrive at 20° of GH elevation in the coronal plane. Here the forearm is already colinear with the axis that is tangent to the latitude (yellow circle), therefore one would measure 0° of axial orientation. Hence, between these two poses, apparent axial rotation dictates that the humerus underwent 90° of internal axial rotation – which does not correspond to the actual rotation about the humerus’ longitudinal axis.