LayNii: A software suite for layer-fMRI
- PMID: 33991698
- PMCID: PMC7615890
- DOI: 10.1016/j.neuroimage.2021.118091
LayNii: A software suite for layer-fMRI
Abstract
High-resolution fMRI in the sub-millimeter regime allows researchers to resolve brain activity across cortical layers and columns non-invasively. While these high-resolution data make it possible to address novel questions of directional information flow within and across brain circuits, the corresponding data analyses are challenged by MRI artifacts, including image blurring, image distortions, low SNR, and restricted coverage. These challenges often result in insufficient spatial accuracy of conventional analysis pipelines. Here we introduce a new software suite that is specifically designed for layer-specific functional MRI: LayNii. This toolbox is a collection of command-line executable programs written in C/C++ and is distributed opensource and as pre-compiled binaries for Linux, Windows, and macOS. LayNii is designed for layer-fMRI data that suffer from SNR and coverage constraints and thus cannot be straightforwardly analyzed in alternative software packages. Some of the most popular programs of LayNii contain 'layerification' and columnarization in the native voxel space of functional data as well as many other layer-fMRI specific analysis tasks: layer-specific smoothing, model-based vein mitigation of GE-BOLD data, quality assessment of artifact dominated sub-millimeter fMRI, as well as analyses of VASO data.
Copyright © 2021 The Author(s). Published by Elsevier Inc. All rights reserved.
Figures


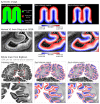


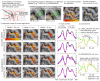
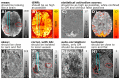
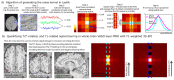

Similar articles
-
Techniques for blood volume fMRI with VASO: From low-resolution mapping towards sub-millimeter layer-dependent applications.Neuroimage. 2018 Jan 1;164:131-143. doi: 10.1016/j.neuroimage.2016.11.039. Epub 2016 Nov 18. Neuroimage. 2018. PMID: 27867088 Free PMC article.
-
Intracortical smoothing of small-voxel fMRI data can provide increased detection power without spatial resolution losses compared to conventional large-voxel fMRI data.Neuroimage. 2019 Apr 1;189:601-614. doi: 10.1016/j.neuroimage.2019.01.054. Epub 2019 Jan 25. Neuroimage. 2019. PMID: 30690157 Free PMC article.
-
A protocol for ultra-high field laminar fMRI in the human brain.STAR Protoc. 2021 Mar 26;2(2):100415. doi: 10.1016/j.xpro.2021.100415. eCollection 2021 Jun 18. STAR Protoc. 2021. PMID: 33851140 Free PMC article.
-
Analysis strategies for high-resolution UHF-fMRI data.Neuroimage. 2018 Mar;168:296-320. doi: 10.1016/j.neuroimage.2017.04.053. Epub 2017 Apr 29. Neuroimage. 2018. PMID: 28461062 Free PMC article. Review.
-
Multi-echo fMRI: A review of applications in fMRI denoising and analysis of BOLD signals.Neuroimage. 2017 Jul 1;154:59-80. doi: 10.1016/j.neuroimage.2017.03.033. Epub 2017 Mar 29. Neuroimage. 2017. PMID: 28363836 Review.
Cited by
-
Multidimensional Alternating Kernel Method for cortical layer segmentation in 3D reconstructed histology.MethodsX. 2024 Apr 5;12:102674. doi: 10.1016/j.mex.2024.102674. eCollection 2024 Jun. MethodsX. 2024. PMID: 38660047 Free PMC article.
-
Dynamic layer-specific processing in the prefrontal cortex during working memory.Commun Biol. 2024 Sep 14;7(1):1140. doi: 10.1038/s42003-024-06780-8. Commun Biol. 2024. PMID: 39277694 Free PMC article.
-
Enabling brain-wide mapping of layer-specific functional connectivity at 3T via layer-dependent fMRI with draining-vein suppression.bioRxiv [Preprint]. 2024 Dec 23:2023.10.24.563835. doi: 10.1101/2023.10.24.563835. bioRxiv. 2024. PMID: 37961360 Free PMC article. Preprint.
-
The temporal specificity of BOLD fMRI is systematically related to anatomical and vascular features of the human brain.Imaging Neurosci (Camb). 2024 Dec 16;2:imag-2-00399. doi: 10.1162/imag_a_00399. eCollection 2024. Imaging Neurosci (Camb). 2024. PMID: 40800285 Free PMC article.
-
Revealing layer-specific cortical activity in human M1 using high-resolution line-scanning fMRI.Imaging Neurosci (Camb). 2025 Feb 21;3:imag_a_00477. doi: 10.1162/imag_a_00477. eCollection 2025. Imaging Neurosci (Camb). 2025. PMID: 40800885 Free PMC article.
References
-
- Aitchison J. The statistical analysis of compositional data. Stat Anal Composit Data. 1986;44(2):139–177.
-
- Amunts K, Lepage C, Borgeat L, Mohlberg H, Dickscheid T, Rousseau MÉ, Bludau S, Bazin PL, Lewis LB, Oros-Peusquens AM, Shah NJ, et al. BigBrain: an ultrahigh-resolution 3D human brain model. Science. 2013;340(6139):1472–1475. - PubMed
-
- Bause J, Polimeni JR, Stelzer J, In MH, Ehses P, Kraemer-Fernandez P, Aghaeifar A, Lacosse E, Pohmann R, Scheffler K. Impact of prospective motion correction, distortion correction methods and large vein bias on the spatial accuracy of cortical laminar fMRI at 9.4 Tesla. Neuroimage. 2020;208 (April 2019) - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

