Micro Air-Pulse Spatial Deformation Spreading Characterizes Degree of Anisotropy in Tissues
- PMID: 33994766
- PMCID: PMC8117953
- DOI: 10.1109/jstqe.2020.3038633
Micro Air-Pulse Spatial Deformation Spreading Characterizes Degree of Anisotropy in Tissues
Abstract
In optical coherence elastography (OCE), air-pulse stimulation has been widely used to produce propagation of mechanical waves for elastic characterization of tissues. In this paper, we propose the use of spatial deformation spreading (SDS) on the surface of samples produced by air-pulse stimulation for the OCE of transverse isotropic tissues. Experiments in isotropic tissue-mimicking phantoms and anisotropic chicken tibialis muscle were conducted using a spectral-domain optical coherence tomography system synchronized with a confocal air-pulse stimulation. SDS measurements were compared with wave speeds values calculated at different propagation angles. We found an approximately linear relationship between shear wave speed and SDS in isotropic phantoms, which was confirmed with predictions made by the numerical integration of a wave propagation model. Experimental measurements in chicken muscle show a good agreement between SDS and surface wave speed taken along and across the axis of symmetry of the tissues, also called degree of anisotropy. In summary, these results demonstrated the capabilities of SDS produced by the air-pulse technique in measuring the shear elastic anisotropy of transverse isotropic tissues.
Keywords: Air-pulse; OCE; anisotropy; chicken tibialis muscle; particle velocity; phantoms; transverse isotropic material; wave propagation.
Figures

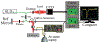
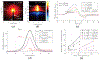

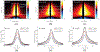


Similar articles
-
Air-pulse optical coherence elastography: how excitation angle affects mechanical wave propagation.Biomed Opt Express. 2025 Mar 11;16(4):1371-1391. doi: 10.1364/BOE.557984. eCollection 2025 Apr 1. Biomed Opt Express. 2025. PMID: 40322015 Free PMC article.
-
Feasibility of optical coherence elastography measurements of shear wave propagation in homogeneous tissue equivalent phantoms.Biomed Opt Express. 2012 May 1;3(5):972-80. doi: 10.1364/BOE.3.000972. Epub 2012 Apr 16. Biomed Opt Express. 2012. PMID: 22567590 Free PMC article.
-
Spatial resolution in dynamic optical coherence elastography.J Biomed Opt. 2019 Sep;24(9):1-16. doi: 10.1117/1.JBO.24.9.096006. J Biomed Opt. 2019. PMID: 31535538 Free PMC article.
-
Quantifying tissue viscoelasticity using optical coherence elastography and the Rayleigh wave model.J Biomed Opt. 2016 Sep 1;21(9):90504. doi: 10.1117/1.JBO.21.9.090504. J Biomed Opt. 2016. PMID: 27653931 Free PMC article.
-
Optical coherence tomography detection of shear wave propagation in inhomogeneous tissue equivalent phantoms and ex-vivo carotid artery samples.Biomed Opt Express. 2014 Feb 26;5(3):895-906. doi: 10.1364/BOE.5.000895. eCollection 2014 Mar 1. Biomed Opt Express. 2014. PMID: 24688822 Free PMC article.
Cited by
-
Full-field noise-correlation elastography for in-plane mechanical anisotropy imaging.Biomed Opt Express. 2024 Mar 26;15(4):2622-2635. doi: 10.1364/BOE.516166. eCollection 2024 Apr 1. Biomed Opt Express. 2024. PMID: 38633096 Free PMC article.
-
Recent advances in optical elastography and emerging opportunities in the basic sciences and translational medicine [Invited].Biomed Opt Express. 2022 Dec 16;14(1):208-248. doi: 10.1364/BOE.468932. eCollection 2023 Jan 1. Biomed Opt Express. 2022. PMID: 36698669 Free PMC article. Review.
-
Wave-based optical coherence elastography: The 10-year perspective.Prog Biomed Eng (Bristol). 2022 Jan;4(1):012007. doi: 10.1088/2516-1091/ac4512. Epub 2022 Jan 14. Prog Biomed Eng (Bristol). 2022. PMID: 35187403 Free PMC article.
-
Introduction to optical coherence elastography: tutorial.J Opt Soc Am A Opt Image Sci Vis. 2022 Mar 1;39(3):418-430. doi: 10.1364/JOSAA.444808. J Opt Soc Am A Opt Image Sci Vis. 2022. PMID: 35297425 Free PMC article.
-
Air-pulse optical coherence elastography: how excitation angle affects mechanical wave propagation.Biomed Opt Express. 2025 Mar 11;16(4):1371-1391. doi: 10.1364/BOE.557984. eCollection 2025 Apr 1. Biomed Opt Express. 2025. PMID: 40322015 Free PMC article.
References
-
- Chadwick P, “Wave propagation in transversely isotropic elastic media - I. Homogeneous plane waves,” Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, vol. 422, pp. 23–66, 1989.
-
- Hoffmeister BK, Handley SM, Wickline SA, and Miller JG, “Ultrasonic determination of the anisotropy of Young’s modulus of fixed tendon and fixed myocardium,” The Journal of the Acoustical Society of America, vol. 100, pp. 3933–3940, 1996. - PubMed
-
- Gennisson J-L, Deffieux T, Macé E, Montaldo G, Fink M, and Tanter M, “Viscoelastic and Anisotropic Mechanical Properties of in vivo Muscle Tissue Assessed by Supersonic Shear Imaging,” Ultrasound in Medicine & Biology, vol. 36, pp. 789–801, 2010/05/01/ 2010. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
