Nonlinear control of networked dynamical systems
- PMID: 33997094
- PMCID: PMC8117950
- DOI: 10.1109/tnse.2020.3032117
Nonlinear control of networked dynamical systems
Abstract
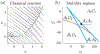
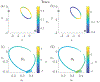
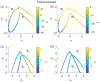
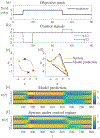
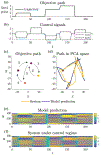
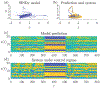
We develop a principled mathematical framework for controlling nonlinear, networked dynamical systems. Our method integrates dimensionality reduction, bifurcation theory, and emerging model discovery tools to find low-dimensional subspaces where feed-forward control can be used to manipulate a system to a desired outcome. The method leverages the fact that many high-dimensional networked systems have many fixed points, allowing for the computation of control signals that will move the system between any pair of fixed points. The sparse identification of nonlinear dynamics (SINDy) algorithm is used to fit a nonlinear dynamical system to the evolution on the dominant, low-rank subspace. This then allows us to use bifurcation theory to find collections of constant control signals that will produce the desired objective path for a prescribed outcome. Specifically, we can destabilize a given fixed point while making the target fixed point an attractor. The discovered control signals can be easily projected back to the original high-dimensional state and control space. We illustrate our nonlinear control procedure on established bistable, low-dimensional biological systems, showing how control signals are found that generate switches between the fixed points. We then demonstrate our control procedure for high-dimensional systems on random high-dimensional networks and Hopfield memory networks.
Keywords: Nonlinear control systems; bifurcation; limit-cycles; open-loop systems; pulse-based switching.
Figures
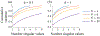

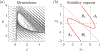




Similar articles
-
Nonlinear Control in the Nematode C. elegans.Front Comput Neurosci. 2021 Jan 22;14:616639. doi: 10.3389/fncom.2020.616639. eCollection 2020. Front Comput Neurosci. 2021. PMID: 33551783 Free PMC article.
-
Koopman Invariant Subspaces and Finite Linear Representations of Nonlinear Dynamical Systems for Control.PLoS One. 2016 Feb 26;11(2):e0150171. doi: 10.1371/journal.pone.0150171. eCollection 2016. PLoS One. 2016. PMID: 26919740 Free PMC article.
-
Sparse identification of nonlinear dynamics for model predictive control in the low-data limit.Proc Math Phys Eng Sci. 2018 Nov;474(2219):20180335. doi: 10.1098/rspa.2018.0335. Epub 2018 Nov 14. Proc Math Phys Eng Sci. 2018. PMID: 30839858 Free PMC article.
-
Hopf Bifurcations in Complex Multiagent Activity: The Signature of Discrete to Rhythmic Behavioral Transitions.Brain Sci. 2020 Aug 9;10(8):536. doi: 10.3390/brainsci10080536. Brain Sci. 2020. PMID: 32784867 Free PMC article. Review.
-
Nonlinear dynamical analysis of EEG and MEG: review of an emerging field.Clin Neurophysiol. 2005 Oct;116(10):2266-301. doi: 10.1016/j.clinph.2005.06.011. Clin Neurophysiol. 2005. PMID: 16115797 Review.
Cited by
-
Nonlinear Control in the Nematode C. elegans.Front Comput Neurosci. 2021 Jan 22;14:616639. doi: 10.3389/fncom.2020.616639. eCollection 2020. Front Comput Neurosci. 2021. PMID: 33551783 Free PMC article.
-
Predicting network dynamics without requiring the knowledge of the interaction graph.Proc Natl Acad Sci U S A. 2022 Nov;119(44):e2205517119. doi: 10.1073/pnas.2205517119. Epub 2022 Oct 24. Proc Natl Acad Sci U S A. 2022. PMID: 36279454 Free PMC article.
-
Optimizing hyperparameters of deep reinforcement learning for autonomous driving based on whale optimization algorithm.PLoS One. 2021 Jun 10;16(6):e0252754. doi: 10.1371/journal.pone.0252754. eCollection 2021. PLoS One. 2021. PMID: 34111168 Free PMC article.
-
Heterogeneous networks: Fair power allocation in LTE-A uplink scenarios.PLoS One. 2021 Jun 21;16(6):e0252421. doi: 10.1371/journal.pone.0252421. eCollection 2021. PLoS One. 2021. PMID: 34153057 Free PMC article.
-
Dynamic Event-Triggered Predictive Control for Interval Type-2 Fuzzy Systems with Imperfect Premise Matching.Entropy (Basel). 2021 Nov 1;23(11):1452. doi: 10.3390/e23111452. Entropy (Basel). 2021. PMID: 34828150 Free PMC article.
References
-
- Rabinovich M, Huerta R, and Laurent G, “Transient dynamics for neural processing,” Science, vol. 321, no. 5885, pp. 48–50, 2008, publisher: American Association for the Advancement of Science. - PubMed
-
- Brunton SL and Kutz JN, Data-driven science and engineering: machine learning, dynamical systems, and control. Cambridge, United Kingdom; New York, NY: Cambridge University Press, 2019.
-
- Kato S, Kaplan H, Schrödel T, Skora S, Lindsay T, Yemini E, Lockery S, and Zimmer M, “Global brain dynamics embed the motor command sequence of Caenorhabditis elegans,” Cell, vol. 163, no. 3, pp. 656–669, Oct. 2015. [Online]. Available: https://linkinghub.elsevier.com/retrieve/pii/S0092867415011964 - PubMed
-
- Marvel SA, Kleinberg J, Kleinberg RD, and Strogatz SH, “Continuous-time model of structural balance,” PNAS, vol. 108, no. 5, pp. 1771–1776, Feb. 2011. [Online]. Available: http://www.pnas.org/content/108/5/1771 - PMC - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
