A fractional order Covid-19 epidemic model with Mittag-Leffler kernel

Abstract

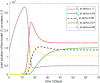
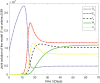
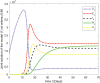
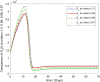
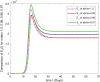
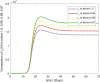
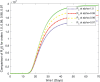
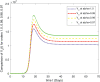
In this article, we are studying fractional-order COVID-19 model for the analytical and computational aspects. The model consists of five compartments including; $``S_c^{″}$ which denotes susceptible class, $``E_c^{″}$ represents exposed population, $``I_c^{″}$ is the class for infected people who have been developed with COVID-19 and can cause spread in the population. The recovered class is denoted by $``R_c^{″}$ and $``V_c^{″}$ is the concentration of COVID-19 virus in the area. The computational study shows us that the spread will be continued for long time and the recovery reduces the infection rate. The numerical scheme is based on the Lagrange's interpolation polynomial and the numerical results for the suggested model are similar to the integer order which gives us the applicability of the numerical scheme and effectiveness of the fractional order derivative.

Keywords: 35R11; Primary 26A33; Secondary 34A08.

Fig. 1

Joint solution of the fractal-fractional model (1) for ${\kappa }_i^{*}=1.0$, for $i=1,2,\dots ,6$.

Fig. 2

Joint solution of the fractal-fractional model (1) for ${\kappa }_i^{*}=0.99$, for $i=1,2,\dots ,6$.

Fig. 3

Joint solution of the fractal-fractional model (1) for ${\kappa }_i^{*}=0.98$, for $i=1,2,\dots ,6$.

Fig. 4

Comparison of $S_c\left(t\right)$ for ${\kappa }_i^{*}=1.0,0.99,0.98,0.97,0.96$, for $i=1,2,\dots ,6$.

Fig. 5

Comparison of $E_c\left(t\right)$ for ${\kappa }_i^{*}=1.0,0.99,0.98,0.97,0.96$, for $i=1,2,\dots ,6$.

Fig. 6

Comparison of $I_c\left(t\right)$ for ${\kappa }_i^{*}=1.0,0.99,0.98,0.97,0.96$, for $i=1,2,\dots ,6$.

Fig. 7

Comparison of $R_c\left(t\right)$ for ${\kappa }_i^{*}=1.0,0.99,0.98,0.97,0.96$, for $i=1,2,\dots ,6$.

Fig. 8

Comparison of $V_c\left(t\right)$ for ${\kappa }_i^{*}=1.0,0.99,0.98,0.97,0.96$, for $i=1,2,\dots ,6$.