Systematic and Random Mapping Errors in Structure - Function Analysis of the Macula

Abstract

Purpose: Quantify the spatial error in mapping perimetric stimuli for structure-function analysis resulting from the choice of mapping scheme and eye movements.

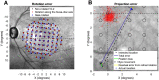
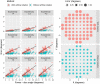
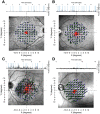
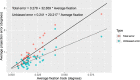
Methods: We analyzed data from 17 healthy and 30 glaucomatous participants. Structural data of the macula were collected with a spectral-domain optical coherence tomography. We extracted eye movement data and projection locations from a fundus tracking perimeter and quantified the retinal location mapping error (distance between the actual and the intended stimulus location in degrees from the fovea) for non-tracked perimetry in a 10-2 grid. First, we evaluated whether rotating the 10-2 grid to match the fovea-disc axis improved mapping accuracy. Second, we analyzed the effect of eccentric fixation, random eye movements, and gaze attraction from seen stimuli on projection accuracy and spread of fixation, measured with the 95% bivariate contour ellipse area (95% BCEA). We used generalized linear mixed models for our statistical analyses.

Results: Rotating the 10-2 grid to match the fovea-disc axis significantly increased the mapping error (P < 0.001). Eye movements evoked by seen stimuli significantly increased the projection error during the test (P < 0.001). Removing such eye movements significantly reduced the 95% BCEA (P < 0.001). Eccentric fixation also significantly contributed to the projection error (P < 0.001), and its effect was larger in glaucoma patients (P < 0.001).

Conclusions: Rotating the perimetric grid to match the fovea-disc axis is not recommended. Fixation eccentricity and instability should be taken into account for structure-function analyses.

Translational relevance: Accounting for fixation can improve structure-function mapping in glaucoma.

Figure 1.

(A) Spectralis fundus picture showing different mapping schemes. All are centered in the fovea. The filled black points represent the non-rotated 10-2 grid (i.e., assuming the horizontal axis of the VF is horizontal on the retina). The filled red points show the 10-2 grid rotated to match the horizontal axis with fovea–disc axis of the subject. Finally, the empty blue circles represent the grid with the real observed rotation from the CMP. The (0,0) coordinate represent the location of the anatomical fovea. (B) Calculation of the projection error. The different segments show different component of the error. The empty black circles represent the intended test locations for the 10-2 grid referenced to the anatomical fovea. The small red dots represent the cloud of fixation positions during the exam. The offset of its center from the anatomical fovea indicates the fixation bias. The (0,0) coordinate represents the location of the anatomical fovea.

Figure 2.

The left panel shows the systematic error introduced by artificial grid rotations at different eccentricities according to the measured fovea–disc angle. The right panel shows the mean error estimated from the model at different locations with and without grid rotation to match the fovea–disc axis.

Figure 3.

Examples from four different subjects of projection errors during a 10-2 VF test. All images are centered on the anatomical fovea. The small red dots represent the cloud of fixation positions during the test. The yellow cross corresponds to the fixation bias. The empty blue circles represent the intended position of the tested location. The small green circles represent the actual location of each projection on the retina, connected to its intended location by a black line. The top track represents the fixation displacement from the initial PRL. The shaded blue vertical bands in the track indicate evoked displacements. (A) Small fixation bias, stable fixation; (B) larger fixation bias, more unstable fixation; (C) extremely chaotic fixation; (D) stable fixation with large fixation bias.

Figure 4.

The left panel shows the fixation bias of each subject. The center of the polar plots represents the anatomical fovea. The dots represent the position of the average fixation during the test. The shaded circle encloses the 95% quantile value of the distance of the center of fixation from the fovea for each group. The panel on the right shows the total error (top) for glaucoma and healthy subjects and the unbiased error (bottom) broken down into evoked and random displacements. The spacing of the vertical axis is in log₁₀ steps.

Figure 5.

Linear regression of the average total and unbiased error according to the average displacement of the fixation track for each subject. Equations of the linear fit are given.

Figure A1.

The red track in the top image represents the gaze displacement evoked by the projection of the stimulus, indicated by the solid white dot, overlaid on the fundus image. The bottom graph shows the same displacement (in blue) in visual field coordinates. The black segment represents the PRL–stimulus direction, whereas the red segment represents the orthogonal projection of the maximum displacement on the black segment (the concordant displacement, CD). (B) Red dots represent the significant positive CDs (evoked by the stimulus). Dashed lines represent the 95% noise limits calculated from the negative CDs and reflected on the positive upper half of the graph. Different noise levels were calculated for projections below (negative on the horizontal axis) and above (negative on the horizontal axis) the threshold.