Mechanistic model of nutrient uptake explains dichotomy between marine oligotrophic and copiotrophic bacteria

Abstract

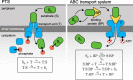
Marine bacterial diversity is immense and believed to be driven in part by trade-offs in metabolic strategies. Here we consider heterotrophs that rely on organic carbon as an energy source and present a molecular-level model of cell metabolism that explains the dichotomy between copiotrophs-which dominate in carbon-rich environments-and oligotrophs-which dominate in carbon-poor environments-as the consequence of trade-offs between nutrient transport systems. While prototypical copiotrophs, like Vibrios, possess numerous phosphotransferase systems (PTS), prototypical oligotrophs, such as SAR11, lack PTS and rely on ATP-binding cassette (ABC) transporters, which use binding proteins. We develop models of both transport systems and use them in proteome allocation problems to predict the optimal nutrient uptake and metabolic strategy as a function of carbon availability. We derive a Michaelis-Menten approximation of ABC transport, analytically demonstrating how the half-saturation concentration is a function of binding protein abundance. We predict that oligotrophs can attain nanomolar half-saturation concentrations using binding proteins with only micromolar dissociation constants and while closely matching transport and metabolic capacities. However, our model predicts that this requires large periplasms and that the slow diffusion of the binding proteins limits uptake. Thus, binding proteins are critical for oligotrophic survival yet severely constrain growth rates. We propose that this trade-off fundamentally shaped the divergent evolution of oligotrophs and copiotrophs.

Fig 1. Schematic of transport systems.

For a nutrient to enter the cytoplasm, a transport unit bound to the inner membrane must expend energy to modify the substrate or translocate the substrate against a concentration gradient. For transport of a sugar by a phosphotransferase system (PTS), the sugar binds directly to the transport unit, and a cascade of specific proteins phosphorylate that particular sugar. For transport of a substrate by an ATP-binding cassette (ABC) transport system, binding proteins in the periplasm first scavenge for and store the substrate in the periplasm. When bound to substrate, a binding protein can then bind to a membrane-bound transport unit, which uses ATP to translocate the substrate. While a single type of binding protein may be able to bind to different substrates, it can bind to only a single, corresponding type of transport unit. To limit the number of free parameters when modeling these two transport systems, we use a simple model of PTS that assumes that binding of the substrate to the transport unit is irreversible. We extend the model for ABC transport to account for the reversible binding of the substrate to the binding protein and the dissociation of the binding protein from the transport unit after translocation.

Fig 2. Maximal uptake rates, half-saturation concentrations, and specific affinities of PTS and ABC transport systems.

We can approximate cytoplasmic uptake rates using the Michaelis–Menten equation: v_c = V_max[S]_p/(K_M+[S]_p), where V_max is the maximal uptake rate and K_M the half-saturation concentration. While the exact solution of the cytoplasmic uptake rate for our model of PTS is in the form of a Michaelis–Menten equation, the exact solution of the uptake rate for ABC transport is not. Because our simulations suggest that the abundance of binding proteins should exceed the abundance of transport units in the oligotrophic conditions where ABC transport is optimal, we make the approximations that (i) [T:S:BP]+[T:BP]≪[BP]_total and (ii) k′₁[T]≪k_0r (Section B in S1 Appendix) to obtain the above estimates for the effective maximal rate and half-saturation concentration. For PTS, the half-saturation concentration is a constant equal to the dissociation constant K_T = k₂/k₁. For ABC transport, the half-saturation concentration depends on both the transport dissociation constant ${K^{\prime }}_{\mathrm{T}}={k^{\prime }}_2{k}_3^{\prime }/\left({k^{\prime }}_1\right(k_2^{\prime }+k_3^{\prime }\left)\right)$ and the binding protein dissociation constant K_D = k′_0r/k′_0f and is additionally a function of the abundance of binding proteins. Under this approximation, the specific affinity a′ = V′_max/K′_M of ABC transport is thus proportional to the product of the abundances of transport units and of binding proteins.

Fig 3. A simple metabolic model tracks the utilization of a generic nutrient by the cell.

The nutrient diffuses into the periplasm via a porous outer membrane and is then transported into the cytoplasm by membrane-bound transport units. The cell uses either transport by PTS, in which the substrate directly binds to the transport unit, or ABC transport, in which the substrate must first bind to a binding protein and then this complex binds to the transport unit. The intracellular substrate is next metabolized by a protein group that transforms the substrate into a precursor (a generic amino acid) that is needed to build the cell. The precursors are used (i) by a membrane biosynthesis protein group to build both the outer and inner membranes and (ii) by ribosomes to make proteins comprising the six protein groups. This model is subject to a number of constraints to determine the proteome allocation that maximizes the steady-state exponential growth rate. While this model does not consider the utilization of carbon for energy, we expanded the model to consider energy to show that differences in the energetic requirements of PTS and ABC transport do not change our results (Section E in S1 Appendix).

Fig 4. Optimal proteome allocation for PTS and ABC transport systems.

Proteome fractions shown are fractions of the proteome available for the four specified protein groups. (A) While it is optimal for cells relying on either PTS or ABC transport systems to devote nearly all of their proteome to transport at low nutrient concentrations, for ABC transport systems, it is the proteome fraction of the binding proteins that increases as nutrient concentration decreases and not the fraction allocated to the membrane-bound transport units. (B) As the nutrient concentration decreases, the optimal maximal uptake of transport increases for PTS but remains constant for ABC transport systems. This results in an increasing ratio of optimal maximal uptake and maximal metabolic rates for transport by PTS as nutrient concentration decreases, while it is optimal for ABC transport systems to maintain this ratio closer to one.

Fig 5. A rate–affinity trade-off.

Plots show the results of proteome allocation problems using either PTS or ABC transport and solved for different extracellular nutrient concentrations (x-axis). We assume that the transport association rate is 100 times lower for ABC transport than for PTS (k′₁ = 0.01k₁) but that the translocation rate as well as the transport unit dissociation constant are equal ($k_2^{\prime }=k_2,K_T^{\prime }=K_T$). We additionally limit the radius of the cell to a minimum of 60 nm, corresponding to a maximum surface-area-to-volume ratio of 50 μm^-1. (A) shows the maximal growth rates achieved using the optimal proteome allocation, and (B) shows the optimal surface-area-to-volume ratio used to achieve those maximal growth rates. ABC transport achieves higher growth rates at low nutrient concentrations because it supports higher substrate affinities per transport proteomic cost, whereas PTS achieves higher growth rates at high nutrient concentrations because it supports higher maximal uptake rates per transport proteomic cost.

Fig 6. The effective half-saturation concentration of ABC transport.

ABC transport systems achieve low optimal half-saturation concentrations (K_eff, magenta curve and axis)—and thus high specific affinities—as nutrient concentrations decrease by maintaining a high surface-area-to-volume ratio and increasing the ratio of the abundance of binding proteins to the abundance of membrane-bound transport units (turquoise curve and axis). For high binding protein to transport unit ratios, the Michaelis-Menten approximation of ABC transport (Eq 6) holds (S1 Fig). At 1 nM, where the binding protein to transport unit ratio is approximately seven, the approximation gives K_eff ≈ 1.5 nM, while the calculated K_eff = 2.9 nM. (For a plot showing how we calculate the effective half-saturation concentration, see S7 Fig).