Using First Principles for Deep Learning and Model-Based Control of Soft Robots

Abstract

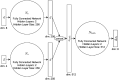
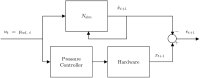
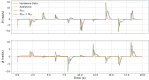
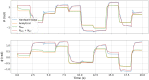
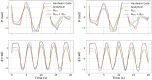
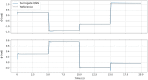
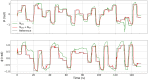
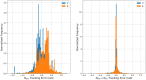
Model-based optimal control of soft robots may enable compliant, underdamped platforms to operate in a repeatable fashion and effectively accomplish tasks that are otherwise impossible for soft robots. Unfortunately, developing accurate analytical dynamic models for soft robots is time-consuming, difficult, and error-prone. Deep learning presents an alternative modeling approach that only requires a time history of system inputs and system states, which can be easily measured or estimated. However, fully relying on empirical or learned models involves collecting large amounts of representative data from a soft robot in order to model the complex state space-a task which may not be feasible in many situations. Furthermore, the exclusive use of empirical models for model-based control can be dangerous if the model does not generalize well. To address these challenges, we propose a hybrid modeling approach that combines machine learning methods with an existing first-principles model in order to improve overall performance for a sampling-based non-linear model predictive controller. We validate this approach on a soft robot platform and demonstrate that performance improves by 52% on average when employing the combined model.

Keywords: data-driven modeling; deep learning; dynamics; error modeling; model predictive control; soft robots.

Figure 1

Photograph of soft robotic continuum joint used for this work. θ and ϕ are the rotations about the joint's x and y axes, respectively.

Figure 2

DNN Architecture, used for both the surrogate model and the error model.

Figure 3

This diagram shows the method used to generate error training data. A random step input pressure trajectory u is sent to the hardware and the states are recorded. The same input trajectory is simulated using the surrogate DNN which takes u and x as inputs. The resulting state trajectory is subtracted from the hardware state trajectory to get the state tracking error over time. This allows the error DNN to predict error given the current state x and the current input u.

Figure 4

Comparison of pressure dynamics between the four different systems used. The dashed line indicates the commanded pressure, while each of the solid lines is the pressure response resulting from the commanded pressure input. Note that the states from the analytical model and the surrogate DNN match well and that when using the combined DNN, the simulation closely resembles the hardware data.

Figure 5

Comparison of velocity dynamics between the four different models used. These velocities are the response resulting from the commanded pressure inputs shown in Figure 4. Note that the surrogate DNN tracks the analytical model well while the combined DNN tracks the hardware data well.

Figure 6

Comparison of joint angle dynamics between the four different models used. These angles are the response resulting from the commanded pressure inputs shown in Figure 4.

Figure 7

Comparison of joint angle dynamics between the four different models used on different test signals. The left column is in response to sine waves in pressure commands and the right column is in response the ramp inputs in pressure commands. Note that the combined DNN, although not trained on sines and ramps, still predicts unmodeled dynamics.

Figure 8

The control performance of NEMPC in simulation. For this trial, the analytical model of the soft robot continuum joint acts as the plant, while NEMPC uses the surrogate DNN as its internal model of the system. Since the surrogate DNN is a very good approximation of the analytical model of the robot, the controller has a near perfect model of the plant, resulting in excellent tracking performance.

Figure 9

Diagram of the experimental setup for the hardware experiments. Also illustrated here is the inherent plasticity of the robot, resulting in a variable offset in θ and ϕ. Over time, the plastic in the pressure chambers deforms and causes the robot to have an equilibrium configuration that is not vertical.

Figure 10

Control diagram for running NEMPC in conjunction with the learned error model. u^* indicates the optimal input chosen by the controller. This input is sent to the embedded pressure controller and we measure pressures p and positions q directly, while estimating $\stackrel{\bullet }{q}$.

Figure 11

Comparison of tracking performance on the physical soft robot continuum joint while using the two categories of DNN model approximation. Note that the control performance of NEMPC while using the combined DNN contains much less steady-state tracking error than the control performance of NEMPC while using the surrogate DNN.

Figure 12

A histogram of the normalized frequency of θ and ϕ tracking error in the hardware experiments. Note that the data gathered while using the surrogate DNN for control has θ error and ϕ error that is biased in both directions away from zero. This is a result of the surrogate DNN's lack of information regarding the offsets in θ and ϕ at equilibrium. Also note the difference in y axis scaling for both histograms.

Figure 13

Comparison of tracking performance on sine (left column) and ramp (right column) test signals using the N_sim + N_err DNN configuration for control. Note that although both DNNs were trained solely on step inputs, the models are able to generalize well to other types of signals.