SPHERIOUSLY? The challenges of estimating sphere radius non-invasively in the human brain from diffusion MRI
- PMID: 34020013
- PMCID: PMC8285594
- DOI: 10.1016/j.neuroimage.2021.118183
SPHERIOUSLY? The challenges of estimating sphere radius non-invasively in the human brain from diffusion MRI
Abstract
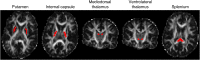
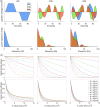
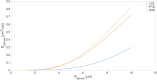
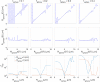
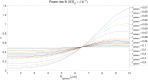
The Soma and Neurite Density Imaging (SANDI) three-compartment model was recently proposed to disentangle cylindrical and spherical geometries, attributed to neurite and soma compartments, respectively, in brain tissue. There are some recent advances in diffusion-weighted MRI signal encoding and analysis (including the use of multiple so-called 'b-tensor' encodings and analysing the signal in the frequency-domain) that have not yet been applied in the context of SANDI. In this work, using: (i) ultra-strong gradients; (ii) a combination of linear, planar, and spherical b-tensor encodings; and (iii) analysing the signal in the frequency domain, three main challenges to robust estimation of sphere size were identified: First, the Rician noise floor in magnitude-reconstructed data biases estimates of sphere properties in a non-uniform fashion. It may cause overestimation or underestimation of the spherical compartment size and density. This can be partly ameliorated by accounting for the noise floor in the estimation routine. Second, even when using the strongest diffusion-encoding gradient strengths available for human MRI, there is an empirical lower bound on the spherical signal fraction and radius that can be detected and estimated robustly. For the experimental setup used here, the lower bound on the sphere signal fraction was approximately 10%. We employed two different ways of establishing the lower bound for spherical radius estimates in white matter. The first, examining power-law relationships between the DW-signal and diffusion weighting in empirical data, yielded a lower bound of 7μm, while the second, pure Monte Carlo simulations, yielded a lower limit of 3μm and in this low radii domain, there is little differentiation in signal attenuation. Third, if there is sensitivity to the transverse intra-cellular diffusivity in cylindrical structures, e.g., axons and cellular projections, then trying to disentangle two diffusion-time-dependencies using one experimental parameter (i.e., change in frequency-content of the encoding waveform) makes spherical radii estimates particularly challenging. We conclude that due to the aforementioned challenges spherical radii estimates may be biased when the corresponding sphere signal fraction is low, which must be considered.
Keywords: Diffusion-weighted imaging; Direction-averaged diffusion signal; Spherical compartment; Three-compartment model; b-tensor encoding.
Copyright © 2021 The Authors. Published by Elsevier Inc. All rights reserved.
Figures



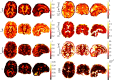

References
-
- Aja-Fernández S., Tristán-Vega A. Influence of noise correlation in multiple-coil statistical models with sum of squares reconstruction. Magnetic Reson. Med. 2012;67(2):580–585. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

