Emergence of canonical functional networks from the structural connectome
- PMID: 34022382
- PMCID: PMC8451304
- DOI: 10.1016/j.neuroimage.2021.118190
Emergence of canonical functional networks from the structural connectome
Abstract
How do functional brain networks emerge from the underlying wiring of the brain? We examine how resting-state functional activation patterns emerge from the underlying connectivity and length of white matter fibers that constitute its "structural connectome". By introducing realistic signal transmission delays along fiber projections, we obtain a complex-valued graph Laplacian matrix that depends on two parameters: coupling strength and oscillation frequency. This complex Laplacian admits a complex-valued eigen-basis in the frequency domain that is highly tunable and capable of reproducing the spatial patterns of canonical functional networks without requiring any detailed neural activity modeling. Specific canonical functional networks can be predicted using linear superposition of small subsets of complex eigenmodes. Using a novel parameter inference procedure we show that the complex Laplacian outperforms the real-valued Laplacian in predicting functional networks. The complex Laplacian eigenmodes therefore constitute a tunable yet parsimonious substrate on which a rich repertoire of realistic functional patterns can emerge. Although brain activity is governed by highly complex nonlinear processes and dense connections, our work suggests that simple extensions of linear models to the complex domain effectively approximate rich macroscopic spatial patterns observable on BOLD fMRI.
Keywords: Complex Laplacian; Functional networks; Graph Laplacian; Structural connectivity.
Copyright © 2021. Published by Elsevier Inc.
Figures
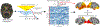



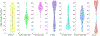
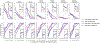
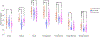
References
Publication types
MeSH terms
Grants and funding
- U01 MH093765/MH/NIMH NIH HHS/United States
- R01 DC017696/DC/NIDCD NIH HHS/United States
- R56 DC019282/DC/NIDCD NIH HHS/United States
- R01 EB022717/EB/NIBIB NIH HHS/United States
- S10 RR019307/RR/NCRR NIH HHS/United States
- R21 NS076171/NS/NINDS NIH HHS/United States
- RF1 AG062196/AG/NIA NIH HHS/United States
- R01 NS100440/NS/NINDS NIH HHS/United States
- R01 DC013979/DC/NIDCD NIH HHS/United States
- S10 RR023043/RR/NCRR NIH HHS/United States
- R01 DC017091/DC/NIDCD NIH HHS/United States
- P41 EB015896/EB/NIBIB NIH HHS/United States
- S10 RR023401/RR/NCRR NIH HHS/United States
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

