Polynomial, piecewise-Linear, Step (PLS): A Simple, Scalable, and Efficient Framework for Modeling Neurons
- PMID: 34025382
- PMCID: PMC8134741
- DOI: 10.3389/fninf.2021.642933
Polynomial, piecewise-Linear, Step (PLS): A Simple, Scalable, and Efficient Framework for Modeling Neurons
Abstract
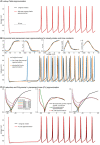
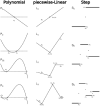
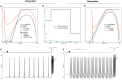
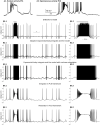
Biological neurons can be modeled with different levels of biophysical/biochemical details. The accuracy with which a model reflects the actual physiological processes and ultimately the information function of a neuron, can range from very detailed to a schematic phenomenological representation. This range exists due to the common problem: one needs to find an optimal trade-off between the level of details needed to capture the necessary information processing in a neuron and the computational load needed to compute 1 s of model time. An increase in modeled network size or model-time, for which the solution should be obtained, makes this trade-off pivotal in model development. Numerical simulations become incredibly challenging when an extensive network with a detailed representation of each neuron needs to be modeled over a long time interval to study slow evolving processes, e.g., development of the thalamocortical circuits. Here we suggest a simple, powerful and flexible approach in which we approximate the right-hand sides of differential equations by combinations of functions from three families: Polynomial, piecewise-Linear, Step (PLS). To obtain a single coherent framework, we provide four core principles in which PLS functions should be combined. We show the rationale behind each of the core principles. Two examples illustrate how to build a conductance-based or phenomenological model using the PLS-framework. We use the first example as a benchmark on three different computational platforms: CPU, GPU, and mobile system-on-chip devices. We show that the PLS-framework speeds up computations without increasing the memory footprint and maintains high model fidelity comparable to the fully-computed model or with lookup-table approximation. We are convinced that the full range of neuron models: from biophysical to phenomenological and even to abstract models, may benefit from using the PLS-framework.
Keywords: CPU; GPU; biophysical models; mobile devices; neurodynamics; neurons; phenomenological models.
Copyright © 2021 Tikidji-Hamburyan and Colonnese.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures
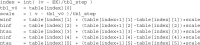
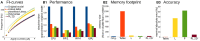



Similar articles
-
Multi-GPU implementation of a VMAT treatment plan optimization algorithm.Med Phys. 2015 Jun;42(6):2841-52. doi: 10.1118/1.4919742. Med Phys. 2015. PMID: 26127037
-
Optimal Piecewise Polynomial Approximation for Minimum Computing Cost by Using Constrained Least Squares.Sensors (Basel). 2024 Jun 20;24(12):3991. doi: 10.3390/s24123991. Sensors (Basel). 2024. PMID: 38931774 Free PMC article.
-
Parallel beamlet dose calculation via beamlet contexts in a distributed multi-GPU framework.Med Phys. 2019 Aug;46(8):3719-3733. doi: 10.1002/mp.13651. Epub 2019 Jun 30. Med Phys. 2019. PMID: 31183871 Free PMC article.
-
Risk management frameworks for human health and environmental risks.J Toxicol Environ Health B Crit Rev. 2003 Nov-Dec;6(6):569-720. doi: 10.1080/10937400390208608. J Toxicol Environ Health B Crit Rev. 2003. PMID: 14698953 Review.
-
Qualitative-Modeling-Based Silicon Neurons and Their Networks.Front Neurosci. 2016 Jun 15;10:273. doi: 10.3389/fnins.2016.00273. eCollection 2016. Front Neurosci. 2016. PMID: 27378842 Free PMC article. Review.
Cited by
-
Reproducibility of biophysical in silico neuron states and spikes from event-based partial histories.PLoS Comput Biol. 2023 Oct 12;19(10):e1011548. doi: 10.1371/journal.pcbi.1011548. eCollection 2023 Oct. PLoS Comput Biol. 2023. PMID: 37824576 Free PMC article.
-
Bridging Hierarchies in Multi-Scale Models of Neural Systems: Look-Up Tables Enable Computationally Efficient Simulations of Non-linear Synaptic Dynamics.Front Comput Neurosci. 2021 Oct 1;15:733155. doi: 10.3389/fncom.2021.733155. eCollection 2021. Front Comput Neurosci. 2021. PMID: 34658827 Free PMC article.
-
Piecewise quadratic neuron model: A tool for close-to-biology spiking neuronal network simulation on dedicated hardware.Front Neurosci. 2023 Jan 9;16:1069133. doi: 10.3389/fnins.2022.1069133. eCollection 2022. Front Neurosci. 2023. PMID: 36699524 Free PMC article.
References
-
- Beyeler M., Carlson K. D., Ting-Shuo Chou, Dutt N., Krichmar J. L. (2015). “Carlsim 3: a user-friendly and highly optimized library for the creation of neurobiologically detailed spiking neural networks,” in 2015 International Joint Conference on Neural Networks (IJCNN) (Killarney: ), 1–8. 10.1109/IJCNN.2015.7280424 - DOI
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

