Introduced populations of ragweed show as much evolutionary potential as native populations

Abstract

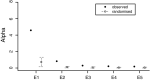
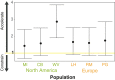
Invasive species are a global economic and ecological problem. They also offer an opportunity to understand evolutionary processes in a colonizing context. The impacts of evolutionary factors, such as genetic variation, on the invasion process are increasingly appreciated, but there remain gaps in the empirical literature. The adaptive potential of populations can be quantified using genetic variance-covariance matrices (G), which encapsulate the heritable genetic variance in a population. Here, we use a multivariate Bayesian approach to assess the adaptive potential of invasive populations of ragweed (Ambrosia artemisiifolia), a serious allergen and agricultural weed. We compared several aspects of genetic architecture and the structure of G matrices between three native and three introduced populations, based on phenotypic data collected in a field common garden experiment. We found moderate differences in the quantitative genetic architecture among populations, but we did not find that introduced populations suffer from a limited adaptive potential or increased genetic constraint compared with native populations. Ragweed has an annual life history, is an obligate outcrosser, and produces very large numbers of seeds and pollen grains. These characteristics, combined with the significant additive genetic variance documented here, suggest ragweed will be able to respond quickly to selection pressures in both its native and introduced ranges.

Keywords: Ambrosia artemisiifolia; G matrices; additive genetic variance; introduced species.

FIGURE 1

Map of Ambrosia artemisiifolia collection sites. Seeds were collected from at least 200 plants in each population in the fall of 2012. Note that the North American samples span latitudes 39.66−44.38 °N, while the French samples span 43.95–45.66 °N

FIGURE 2

Heritability estimates of ragweed (a) early height, (b) branch number, (c) final height, and (d) flowering time. North American populations are to the left of the red line (from north to south: MI, CB, WV), and European populations are to the right of the red line (from north to south: LH, RM, PG). Mean posterior estimates are shown in black (circles), and randomized mean estimates are white circles with the 95% intervals shown as dashed lines. For heritability estimates, the genetic variance within each population is divided by the phenotypic variance for that population, rather than for the total experiment

FIGURE 3

Results from the Krzanowski analysis using only the four phenotypic traits (early height, final height, branch number, and flowering time) (a) and including estimates for male and female fitness (b). The eigenvalues (mean and 95% HPD interval) of each of the first two (a) or three (b) eigenvectors of H are shown for the observed (closed circle, solid lines) and randomized (open circles, dashed lines). Values closer to 6 (the number of populations compared) indicate greater similarity in multivariate directions of genetic variation

FIGURE 4

Results of tensor analysis of G matrices for six A. artemisiifolia populations. Eigenvalues of eigentensors for posterior mean S (the covariance matrix representing the fourth‐order covariance tensor). The amount of variance (alpha) accounted for by each eigentensor is shown for G matrices of the six observed (solid circle) and randomized (dashed line and open circle) populations. The error bars are the 95% HPD intervals generated using 500,000 MCMC total iterations for 1000 randomized phenotypes

FIGURE 5

Predicted response to selection for final height predicted by solving the breeder's equation for six ragweed populations (three native (MI, CB, and WV) and three introduced (LH, RM, and PG)). Final height is shown in standard deviation units

FIGURE 6

R metric for three native (MI, CB, and WV) and three introduced (LH, RM, and PG) ragweed populations. Values greater than 1 indicate that evolution would be accelerated by genetic correlations, and values less than 1 indicate they would be constrained by genetic correlations. Error bars depict the 5th and 95th percentile