Dynamic fingerprint of fractionalized excitations in single-crystalline Cu3Zn(OH)6FBr

Abstract

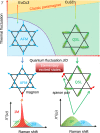
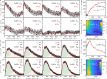
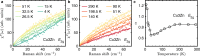
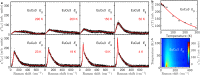
Beyond the absence of long-range magnetic orders, the most prominent feature of the elusive quantum spin liquid (QSL) state is the existence of fractionalized spin excitations, i.e., spinons. When the system orders, the spin-wave excitation appears as the bound state of the spinon-antispinon pair. Although scarcely reported, a direct comparison between similar compounds illustrates the evolution from spinon to magnon. Here, we perform the Raman scattering on single crystals of two quantum kagome antiferromagnets, of which one is the kagome QSL candidate Cu₃Zn(OH)₆FBr, and another is an antiferromagnetically ordered compound EuCu₃(OH)₆Cl₃. In Cu₃Zn(OH)₆FBr, we identify a unique one spinon-antispinon pair component in the E_2g magnetic Raman continuum, providing strong evidence for deconfined spinon excitations. In contrast, a sharp magnon peak emerges from the one-pair spinon continuum in the E_g magnetic Raman response once EuCu₃(OH)₆Cl₃ undergoes the antiferromagnetic order transition. From the comparative Raman studies, we can regard the magnon mode as the spinon-antispinon bound state, and the spinon confinement drives the magnetic ordering.

Fig. 1. Schematical comparative Raman responses for the AFM and QSL states.

With a large DM interaction D, the kagome antiferromagnet develops a chiral 120° AFM ground state. Increasing J/D, the fluctuation of the kagome system increases, driving the system into the QSL state. By increasing the temperature, the thermal fluctuation melts the magnetic order and turns the system into the classic paramagnetic state at high temperatures. Cu₃Zn and EuCu₃ have the QSL and AFM ground states, and allow spinon and magnon excitations, respectively. Magnetic Raman scattering measures different elementary excited states in the two different ground states. Here 1P and 2P denote the one-pair and two-pair spinon excitations, respectively. 1M and 2M in AFM ordered state denote the one- and two-magnon excitations, respectively. The 1M Raman peak in AFM measures the magnon while the 1P Raman continuum in QSL probes the spinon excitations. The shadow background of the 1M peak, marked as `1P', denotes the continuum above T_N in EuCu₃, mimicking the 1P continuum in the QSL state.

Fig. 2. Temperature dependent and ARPR spectra in Cu₃Zn.

a Temperature evolution of unpolarized Raman spectra in Cu₃Zn. The inset is the photo of single crystals. ARPR intensity for low-energy continua (b), the Br⁻E_2g phonon (75 cm⁻¹) (c), and the O²⁻A_1g phonon (429 cm⁻¹) (d). The dash-dotted lines are the corresponding theoretical curves based on the C₃ rotation symmetry.

Fig. 3. Temperature dependent magnetic Raman continua in Cu₃Zn.

a The A_1g Raman susceptibility ${\chi }_{A_{\mathrm{1g}}}^{{}^{″}}={\chi }_{\mathrm{XX}}^{{}^{″}}-{\chi }_{\mathrm{XY}}^{{}^{″}}$. The solid lines are guides to the eye. b Temperature dependence of the A_1g static Raman susceptibility ${\chi }_{A_{\mathrm{1g}}}^{\prime }\left(T\right)=\frac{2}{\pi }{\int }_{10{\mathrm{cm}}^{-1}}^{400{\mathrm{cm}}^{-1}}\frac{{\chi }_{A_{\mathrm{1g}}}^{{}^{″}}\left(\omega \right)}{\omega }d\omega$. The solid line is a thermally activated function. c Color map of ${\chi }_{A_{\mathrm{1g}}}^{{}^{″}}\left(\omega ,T\right)$. d The E_2g Raman response function ${\chi }_{E_{\mathrm{2g}}}^{{}^{″}}={\chi }_{\mathrm{XY}}^{\prime }$. The solid lines are guides to the eye. The light green and pink shadow marked as “1P” and “2P” represent the one-pair and two-pair components of Raman continuum. e Temperature dependence of the E_2g static Raman susceptibility ${\chi }_{E_{\mathrm{2g}}}^{\prime }\left(T\right)=\frac{2}{\pi }{\int }_{10{\mathrm{cm}}^{-1}}^{780{\mathrm{cm}}^{-1}}\frac{{\chi }_{E_{\mathrm{2g}}}^{{}^{″}}\left(\omega \right)}{\omega }d\omega$. The solid line is a guide to the eye. f Color map of ${\chi }_{E_{\mathrm{2g}}}^{{}^{″}}\left(\omega ,T\right)$.

Fig. 4. Power-law behavior for E_2g magnetic Raman continua at low frequency in Cu₃Zn.

a, b are power-law fitting of ${\chi }_{E_{\mathrm{2g}}}^{{}^{″}}\left(\omega \right)\propto {\omega }^{\alpha }$ at low and high temperatures, respectively. c Temperature-dependent exponent α for the power-law fitting.

Fig. 5. Temperature dependent E_g magnetic Raman continua in EuCu₃.

a The E_g Raman susceptibility ${\chi }_{E_{\mathrm{g}}}^{{}^{″}}={\chi }_{\mathrm{XY}}^{{}^{″}}$. The solid lines are guides to the eye. A sharp magnon peak appears in the E_g magnetic Raman continuum below the magnetic transition temperature T_N = 17 K. b Temperature dependence of the static Raman susceptibility in the E_g channel ${\chi }_{E_{\mathrm{g}}}^{\prime }\left(T\right)=\frac{2}{\pi }{\int }_{10{\mathrm{cm}}^{-1}}^{780{\mathrm{cm}}^{-1}}\frac{{\chi }_{E_{\mathrm{g}}}^{{}^{″}}\left(\omega ,T\right)}{\omega }d\omega$. The solid line is a guide to the eye. c Color map of ${\chi }_{E_{\mathrm{g}}}^{{}^{″}}\left(\omega ,T\right)$.

Fig. 6. Comparative Raman studies of EuCu₃ and Cu₃Zn.

We select the E_g magnetic Raman continua in EuCu₃ at several temperatures. For a comparison, we also plot the E_2g magnetic Raman continuum in Cu₃Zn at 4 K with the Raman shift scaled by the superexchange energy ratio of 1.9.