Minimal and Maximal Models to Quantitate Glucose Metabolism: Tools to Measure, to Simulate and to Run in Silico Clinical Trials

Abstract

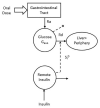
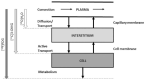
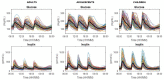
Several models have been proposed to describe the glucose system at whole-body, organ/tissue and cellular level, designed to measure non-accessible parameters (minimal models), to simulate system behavior and run in silico clinical trials (maximal models). Here, we will review the authors' work, by putting it into a concise historical background. We will discuss first the parametric portrait provided by the oral minimal models-building on the classical intravenous glucose tolerance test minimal models-to measure otherwise non-accessible key parameters like insulin sensitivity and beta-cell responsivity from a physiological oral test, the mixed meal or the oral glucose tolerance tests, and what can be gained by adding a tracer to the oral glucose dose. These models were used in various pathophysiological studies, which we will briefly review. A deeper understanding of insulin sensitivity can be gained by measuring insulin action in the skeletal muscle. This requires the use of isotopic tracers: both the classical multiple-tracer dilution and the positron emission tomography techniques are discussed, which quantitate the effect of insulin on the individual steps of glucose metabolism, that is, bidirectional transport plasma-interstitium, and phosphorylation. Finally, we will present a cellular model of insulin secretion that, using a multiscale modeling approach, highlights the relations between minimal model indices and subcellular secretory events. In terms of maximal models, we will move from a parametric to a flux portrait of the system by discussing the triple tracer meal protocol implemented with the tracer-to-tracee clamp technique. This allows to arrive at quasi-model independent measurement of glucose rate of appearance (Ra), endogenous glucose production (EGP), and glucose rate of disappearance (Rd). Both the fast absorbing simple carbs and the slow absorbing complex carbs are discussed. This rich data base has allowed us to build the UVA/Padova Type 1 diabetes and the Padova Type 2 diabetes large scale simulators. In particular, the UVA/Padova Type 1 simulator proved to be a very useful tool to safely and effectively test in silico closed-loop control algorithms for an artificial pancreas (AP). This was the first and unique simulator of the glucose system accepted by the U.S. Food and Drug Administration as a substitute to animal trials for in silico testing AP algorithms. Recent uses of the simulator have looked at glucose sensors for non-adjunctive use and new insulin molecules.

Keywords: diabetes; in silico simulation; insulin action; insulin secretion; multiscale modeling; stabilized tracers.

Figure 1.

Top panel: Mixed meal (left) and OGTT(right) plasma glucose (top), insulin (middle) and C-peptide (bottom) in the same subject. Bottom panel: Partition analysis of the system allows to separately estimate insulin sensitivity, beta-cell responsivity and hepatic extraction without the confounding effect of the 2 other parameters. Relevant input and output signals of the 3 models are shown (adapted from).

Figure 2.

The oral glucose minimal models which allow to estimate insulin sensitivity (top panel), beta-cell responsivity (middle panel) and hepatic insulin extraction (bottom panel (adapted from).

Figure 3.

Schematic diagram to illustrate the importance of expressing beta-cell responsivity in relation to insulin sensitivity is illustrated by using the disposition index metric, that is, the product of beta-cell responsivity times insulin sensitivity is assumed to be a constant. Left panel: A normal subject (state I) reacts to impaired insulin sensitivity by increasing beta-cell responsivity (state II) while a subject with impaired tolerance does not (state 2). In state II beta-cell responsivity is increased but the disposition index is unchanged, and normal glucose tolerance is retained normal, while in state 2 beta-cell responsivity is normal but not adequate to compensate the decreased insulin sensitivity (state 2), and glucose intolerance is developed. Right panel: Impaired glucose tolerance can arise due to defects of beta-cell responsivity and/or defects of insulin sensitivity. In this hypothetical example, subject X is intolerant due to her/his poor beta-beta-cell function, while subject Y has poor insulin sensitivity. The ability to dissect the underlying physiological defects (insulin sensitivity or beta-cell responsivity) allows to optimize medical treatments (adapted from).

Figure 4.

The labeled oral minimal model which allows to estimate disposal insulin sensitivity (adapted from ).

Figure 5.

Skeletal muscle major glucose processes: diffusion to/from the intersitium, active transport in and out of the cell, and phosphorylation/metabolism.

Figure 6.

The 5k model of [F]FDG in skeletal muscle: C_p is [F]FDG plasma arterial concentration, C_c extracellular concentration of [F]FDG normalized to tissue volume, C_e [F]FDG tissue concentration, Cm [F]FDG—6—P tissue concentration, C total F activity concentration in the ROI, K₁ [ml/ml/min] and k₂ [min⁻¹] the exchange between plasma and extracellular space, k₃ [min⁻] and k₄ [min⁻¹] transport in and out of cell, k₅ [min⁻¹] phosphorylation.

Figure 7.

The 3 PET tracer protocol to study glucose diffusion through capillary membrane, active transport into the cells and metabolism.

Figure 8.

Left panel: Grodsky’s model with a large reserve pool and a small labile pool of insulin packets with different thresholds. Right panel: The model with a pool of docked insulin granules (D), a readily releasable pool (RRP) and a pool of fused granules (F) releasing insulin. The model assumes that beta-cells have different activation threshold with respect to the glucose concentration (G) by distinguishing between RRP granules in active cells (denoted H(G), filled circles) and in silent cells (open circles) (adapted from and).

Figure 9.

Scheme of the dual (left) and the triple tracer (right panel) protocol. In the dual tracer protocol the first tracer is mixed with the meal and the second one is infused intravenously with a constant rate. In the triple tracer protocol the first tracer is mixed with the meal, the second one is infused intravenously trying to mimic the expected pattern of EGP and the third one is infused intravenously trying to mimic the expected pattern of Ra_meal.

Figure 10.

TTR_exo (in dpm/µmol) (upper) and TTR_end (in dpm/µmol) (lower panel) used in the triple tracer methods in 8 healthy subjects. TTR are in dpm/µmol since in this study the i.v. infused tracer is radioactive. Vertical bars represent standard error (adapted from).

Figure 11.

Scheme of latest version of the UVa/Padova T1D simulator, incorporating time-varying parameters describing intraday variability of insulin sensitivity and dawn phenomenon. The simulator also includes various insulin delivery routes (subcutaneous fast-acting insulin, intradermal and inhaled insulins) and glucose monitoring devices (both CGM and SMBG) (adapted from).

Figure 12.

Simulated plasma glucose (upper) and insulin (lower panels) in the 100 in silico adults (left), adolescents (middle), and children (right panels) available in the UVa/Padova T1D simulator. Subjects underwent a 24-hour scenario with 3 identical meals (60 g of CHO) at 7:00 am, 1:00 pm, 7:00 pm, respectively, and received optimal subcutaneous insulin basal and bolus (adapted from).

Figure 13.

The use of the UVa/Padova T1D simulator for testing new molecules: once the PK-PD of the molecule under investigation is incorporated in the simulator, simulations can be run predicting clinical outcomes, for example, optimal dosing, safety and efficacy.

Figure 14.

Block-scheme representing the T1D patient decision simulator. Arrows entering each block are inputs, while arrows exiting are causally-related outputs. The input of the simulator is the sequence of meals, while the output is the BG concentration profile. The simulator includes parameters describing the patient’s physiology and therapy. The picture reports representative time courses for meals in input and BG in output for a simple scenario in which the patient takes 50 g for breakfast at 07:00 am (adapted from).

Figure 15.

Upper panel: average (filled circle) ± standard deviation (SD, shaded area) plasma glucose, insulin and C-peptide concentration and estimated endogenous glucose production (EGP), glucose rate of appearance (Ra_meal) and glucose utilization (U) in T2D subjects (N = 51). Lower panel: scheme of the T2D simulation model. Metabolic fluxes are indicated with continuous lines, while control actions are represented by dashed lines. Adapted from.