Analysis of Indoor Radon Data Using Bayesian, Random Binning, and Maximum Entropy Methods
- PMID: 34035781
- PMCID: PMC8132103
- DOI: 10.1177/15593258211009337
Analysis of Indoor Radon Data Using Bayesian, Random Binning, and Maximum Entropy Methods
Abstract
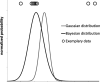
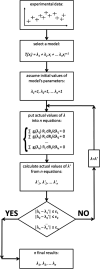
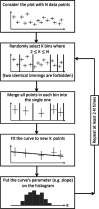
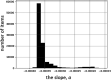
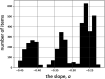
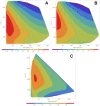
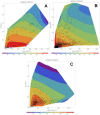
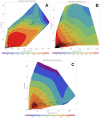
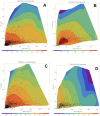
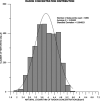
Three statistical methods: Bayesian, randomized data binning and Maximum Entropy Method (MEM) are described and applied in the analysis of US radon data taken from the US registry. Two confounding factors-elevation of inhabited dwellings, and UVB (ultra-violet B) radiation exposure-were considered to be most correlated with the frequency of lung cancer occurrence. MEM was found to be particularly useful in extracting meaningful results from epidemiology data containing such confounding factors. In model testing, MEM proved to be more effective than the least-squares method (even via Bayesian analysis) or multi-parameter analysis, routinely applied in epidemiology. Our analysis of the available residential radon epidemiology data consistently demonstrates that the relative number of lung cancers decreases with increasing radon concentrations up to about 200 Bq/m3, also decreasing with increasing altitude at which inhabitants live. Correlation between UVB intensity and lung cancer has also been demonstrated.
Keywords: Bayesian; Maximum Entropy Method; Monte Carlo; radon analysis; radon risk; risk analysis.
© The Author(s) 2021.
Conflict of interest statement
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Figures


Similar articles
-
Lung cancer risk from radon exposure in dwellings in Sweden: how many cases can be prevented if radon levels are lowered?Cancer Causes Control. 2015 Apr;26(4):541-7. doi: 10.1007/s10552-015-0531-6. Epub 2015 Feb 13. Cancer Causes Control. 2015. PMID: 25677843 Free PMC article.
-
Residential radon and lung cancer in Sweden: risk analysis accounting for random error in the exposure assessment.Health Phys. 1997 Feb;72(2):269-76. doi: 10.1097/00004032-199702000-00010. Health Phys. 1997. PMID: 9003712
-
RADON AND THORON PROGENY IN DUTCH DWELLINGS.Radiat Prot Dosimetry. 2018 Sep 1;181(1):11-14. doi: 10.1093/rpd/ncy093. Radiat Prot Dosimetry. 2018. PMID: 29931357
-
Predicted indoor radon concentrations from a Monte Carlo simulation of 1,000,000 granite countertop purchases.J Radiol Prot. 2013 Mar;33(1):151-62. doi: 10.1088/0952-4746/33/1/151. Epub 2013 Jan 7. J Radiol Prot. 2013. PMID: 23295242
-
Radon and Thoron; Radioactive Gases Lurking in Earthen Houses in Rural Kenya.Front Public Health. 2019 May 8;7:113. doi: 10.3389/fpubh.2019.00113. eCollection 2019. Front Public Health. 2019. PMID: 31134175 Free PMC article. Review.
Cited by
-
Assessment of indoor radon distribution and seasonal variation within the Kpando Municipality of Volta Region, Ghana.PLoS One. 2024 Feb 27;19(2):e0299072. doi: 10.1371/journal.pone.0299072. eCollection 2024. PLoS One. 2024. PMID: 38412163 Free PMC article.
-
Correlative links between natural radiation and life expectancy in the US population.Biogerontology. 2022 Aug;23(4):425-430. doi: 10.1007/s10522-022-09971-0. Epub 2022 Jun 21. Biogerontology. 2022. PMID: 35727470
-
The enduring legacy of Marie Curie: impacts of radium in 21st century radiological and medical sciences.Int J Radiat Biol. 2022;98(3):267-275. doi: 10.1080/09553002.2022.2027542. Epub 2022 Feb 2. Int J Radiat Biol. 2022. PMID: 35030065 Free PMC article. Review.
-
Designing an Indoor Radon Risk Exposure Indicator (IRREI): An Evaluation Tool for Risk Management and Communication in the IoT Age.Int J Environ Res Public Health. 2021 Jul 26;18(15):7907. doi: 10.3390/ijerph18157907. Int J Environ Res Public Health. 2021. PMID: 34360202 Free PMC article.
References
-
- Council Directive 2013/59/Euratom of 5 December 2013. Laying down basic safety standards for protection against the dangers arising from exposure to ionising radiation. Published 2013. Accessed March 1, 2021. https://eur-lex.europa.eu/eli/dir/2013/59/oj
-
- Vogeltanz-Holm N, Schwartz GG. Radon and lung cancer: what does the public really know? J Environ Radioact. 2018;192:26–31. - PubMed
-
- Rodríguez-Martínez Á, Torres-Durán M, Barros-Dios JM, Ruano-Ravina A. Residential radon and small cell lung cancer. A systematic review. Cancer Lett. 2018;426:57–62. doi:10.1016/j.canlet.2018.04.003 - PubMed
-
- Dempsey S, Lyons S, Nolan A. High radon areas and lung cancer prevalence: evidence from Ireland. J Environ Radioact. 2018;182:12–19. - PubMed
LinkOut - more resources
Full Text Sources
Other Literature Sources

