Aperiodic stochastic resonance in neural information processing with Gaussian colored noise

Abstract

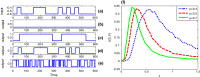
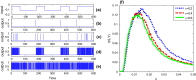
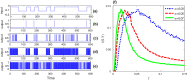
The aim of this paper is to explore the phenomenon of aperiodic stochastic resonance in neural systems with colored noise. For nonlinear dynamical systems driven by Gaussian colored noise, we prove that the stochastic sample trajectory can converge to the corresponding deterministic trajectory as noise intensity tends to zero in mean square, under global and local Lipschitz conditions, respectively. Then, following forbidden interval theorem we predict the phenomenon of aperiodic stochastic resonance in bistable and excitable neural systems. Two neuron models are further used to verify the theoretical prediction. Moreover, we disclose the phenomenon of aperiodic stochastic resonance induced by correlation time and this finding suggests that adjusting noise correlation might be a biologically more plausible mechanism in neural signal processing.

Keywords: Aperiodic stochastic resonance; Local Lipschitz condition; Mutual information; Ornstein–Ulenbeck process.

Fig. 1

Schemata of the vector field function of $f(x)$ (blue solid line). The value of the above dot line is 0.63, and the value of the bottom dotted line is 0.37. In the figure, the intersection of the dash line with the S-shaped curve stands for the equilibrium points, and the one-order derivative of the vector field just is the resultant slope of tangent line. Since two of the three slopes are negative and one is positive, two of the three equilibrium points are stable, and one is unstable. (Color figure online)

Fig. 2

Stochastic resonance in the bistable neuron model with quantized output. The binary signal is shown in panel (a). Here $A=-0.6$, $B=-0.4$ and $p=0.7$. Since the input signal is subthreshold, there is no 1 in the quantized output when the Gaussian colored noise is absent ($\sigma =0$,$\tau =0.4$), as shown in panel (b). As the noise intensity of the Gaussian colored noise is introduced, more and more “1s” occur in the quantized output, as shown in panel (c) ($\sigma =0.1$, $\tau =0.4$), (d) ($\sigma =0.4$, $\tau =0.4$) and (e) ($\sigma =1$, $\tau =0.4$), but obviously too much Gaussian colored noise will reduce the input–output coherence, so there is a mono-peak structure in the curves of mutual information via noise intensity as shown in panel (f): $\tau =0.2$(blue dot curve),$\tau =0.4$(red broken curve) and $\tau =0.6$ (green solid curve). (Color figure online)

Fig. 3

Stochastic resonance in the bistable neuron model with quantized output. The binary signal is shown in panel (a). Here $A=-0.6$, $B=-0.4$ and $p=0.7$. There is no 1 in the quantized output when the correlation time constant of Gaussian colored noise is close to zero ($\tau =0.001$,$\sigma =0.3$), as shown in panel (b). As the correlation time constant increases, more and more “1s” occur in the quantized output, as shown in panel (c) ($\tau =0.2$, $\sigma =0.3$) (d) ($\tau =0.5$, $\sigma =0.3$), and (e) ($\tau =1.5$, $\sigma =0.3$), but obviously too large correlation time constant will reduce the input–output coherence, so there is a mono-peak structure in the curves of mutual information via correlation time constant as shown in panel (f): $\sigma =0.3$ (blue dot curve), $\sigma =0.5$ (red broken curve) and $\sigma =0.7$(green solid curve). (Color figure online)

Fig. 4

Mutual information between input signal $S$ and quantized output signal $Y$ as a function of (a) the noise intensity $\sigma$ with and (b) correlation time constant $\tau$ under different duration time parameters for the input signal. Here $A=-0.6$, $B=-0.4$ and $p=0.7$

Fig. 5

Stochastic resonance in the FitzHugh–Nagumo neuron model. Here $g(v)=1$,$A=-0.035$, $B=-0.125$ and $p=0.7$. (a) The subthreshold binary signal. (b) Output spikes when the Gaussian colored noise is absent ($\sigma =0$,$\tau =0.4$). (c) Output spikes when the noise intensity of Gaussian colored noise is small ($\sigma =0.003$, $\tau =0.4$). (d) Stochastic resonance effect: Output spikes when the noise intensity of Gaussian colored noise is moderate ($\sigma =0.01$, $\tau =0.4$). (e) Output spikes when the noise intensity of Gaussian colored noise is large ($\sigma =0.04$,$\tau =0.4$). Obviously too much Gaussian colored noise will reduce the input–output coherence, so there is a mono-peak structure in the curves of mutual information via noise intensity as shown in panel (f): $\tau =0.2$ (blue dot curve),$\tau =0.4$(red broken curve) and $\tau =0.6$ (green solid curve). (Color figure online)

Fig. 6

Stochastic resonance in the FitzHugh–Nagumo neuron model. Here $g(v)=1$, $A=-0.035$, $B=-0.125$ and $p=0.7$. (a) The subthreshold binary signal. (b) Output spikes when the correlation time constant of Gaussian colored noise is close to zero ($\tau =0.001$,$\sigma =0.03$). (c) Output spikes when the correlation time constant is small ($\tau =0.01$, $\sigma =0.03$). (d) Stochastic resonance effect: Output spikes when the correlation time constant is moderate ($\tau =0.05$, $\sigma =0.03$). (e) Output spikes when the correlation time constant is large ($\tau =0.2$, $\sigma =0.03$). Obviously too large correlation time constant will reduce the input–output coherence, so there is a mono-peak structure in the curves of mutual information via correlation time constant as shown in panel (f): $\sigma =0.03$ (blue dot curve), $\sigma =0.05$ (red broken curve) and $\sigma =0.07$ (green solid curve). (Color figure online)

Fig. 7

Mutual information between input signal $S$ and output spike train $Y$ as a function of (a) the noise intensity $\sigma$ and (b) correlation time constant $\tau$. Here $g(v)=\frac{v^2}{\sqrt{1+v^4}}$, $A=-0.035$, $B=-0.125$ and $p=0.7$. (Color figure online)