Bayesian Inference of Vocal Fold Material Properties from Glottal Area Waveforms Using a 2D Finite Element Model
- PMID: 34046213
- PMCID: PMC8153513
- DOI: 10.3390/app9132735
Bayesian Inference of Vocal Fold Material Properties from Glottal Area Waveforms Using a 2D Finite Element Model
Abstract
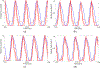
Bayesian estimation has been previously demonstrated as a viable method for developing subject-specific vocal fold models from observations of the glottal area waveform. These prior efforts, however, have been restricted to lumped-element fitting models and synthetic observation data. The indirect relationship between the lumped-element parameters and physical tissue properties renders extracting the latter from the former difficult. Herein we propose a finite element fitting model, which treats the vocal folds as a viscoelastic deformable body comprised of three layers. Using the glottal area waveforms generated by self-oscillating silicone vocal folds we directly estimate the elastic moduli, density, and other material properties of the silicone folds using a Bayesian importance sampling approach. Estimated material properties agree with the "ground truth" experimental values to within 3% for most parameters. By considering cases with varying subglottal pressure and medial compression we demonstrate that the finite element model coupled with Bayesian estimation is sufficiently sensitive to distinguish between experimental configurations. Additional information not available experimentally, namely, contact pressures, are extracted from the developed finite element models. The contact pressures are found to increase with medial compression and subglottal pressure, in agreement with expectation.
Keywords: Bayesian inverse analysis; finite element analysis; patient-specific modeling; silicone vocal fold models.
Conflict of interest statement
Conflicts of Interest: The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Figures
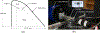



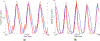


References
-
- Story BH An overview of the physiology, physics and modeling of the sound source for vowels. Acoust. Sci. Technol 2002, 23, 195–206.
-
- Birkholz P; Kroger B; Neuschaefer-Rube C Model-based reproduction of articulatory trajectories for consonant–vowel sequences. IEEE Trans. Audio Speech Lang. Process 2011, 19, 1422–1433.
Grants and funding
LinkOut - more resources
Full Text Sources
