The Stochastic Nature of Functional Responses

Abstract

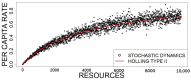
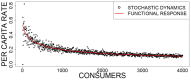
Functional responses are non-linear functions commonly used to describe the variation in the rate of consumption of resources by a consumer. They have been widely used in both theoretical and empirical studies, but a comprehensive understanding of their parameters at different levels of description remains elusive. Here, by depicting consumers and resources as stochastic systems of interacting particles, we present a minimal set of reactions for consumer resource dynamics. We rigorously derived the corresponding system of ODEs, from which we obtained via asymptotic expansions classical 2D consumer-resource dynamics, characterized by different functional responses. We also derived functional responses by focusing on the subset of reactions describing only the feeding process. This involves fixing the total number of consumers and resources, which we call chemostatic conditions. By comparing these two ways of deriving functional responses, we showed that classical functional response parameters in effective 2D consumer-resource dynamics differ from the same parameters obtained by measuring (or deriving) functional responses for typical feeding experiments under chemostatic conditions, which points to potential errors in interpreting empirical data. We finally discuss possible generalizations of our models to systems with multiple consumers and more complex population structures, including spatial dynamics. Our stochastic approach builds on fundamental ecological processes and has natural connections to basic ecological theory.

Keywords: Beddington–DeAngelis functional response; Holling type II and type III functional responses; feeding experiments; stochastic consumer-resource dynamics; system’s size expansion.

Figure 1

Transcritical bifurcation for ${\lambda }_R=2\beta$, ${\lambda }_A=0$, and ${\delta }_A=3\alpha /2$. Here, the vertical axis stands for the scaled resource abundance $f_R$, and the horizontal axis represents the control parameter $q=1-{\delta }_R/\beta$. For $q<q^{\star }=13/6$, the (upper) solution $f_R^{\left(2\right)}=3/2$ is stable and for $q>q^{\star }$ stability changes and $f_R^{\left(1\right)}=\frac{1}{2}\left(q-2+\sqrt{{(2-q)}^2+8}\right)$ becomes the stable resource scaled abundance. Observe that for $q>q^{\star }$, consumer, pair, and triplet abundances become equal to zero in the stable branch. Stable (unstable) solutions are marked with full (dashed) lines.

Figure 2

Parameter space showing transitions between different stability regimes for ${\lambda }_R=0$, ${\lambda }_A=0$, and ${\delta }_R=0$. In this case, the transcritical bifurcation threshold (32) reduces to the vertical line $\alpha ={\delta }_A$. The threshold ${\alpha }_c$ (cf. Equation (42)) for the Hopf bifurcation is the limit (for $\beta \to 0$) of the line that separates stable oscillations and limit cycles. The remaining lines were computed by numerical evaluation of the Jacobian eigenvalues.

Figure 3

Plot of the per capita feeding rate of the stochastic process defined by the reactions (57)–(58). Simulations were carried out using the Gillespie algorithm with 10,000 steps, while the rates (black dots) were calculated, after a transient of 5000 steps, for different values of resource concentrations and compared with the functional response given by Equation (72) (red line). The simulation parameters are $\beta =1.5$, ${\delta }_A=1$, $\alpha =2.5$, $\nu =1$, and $N=$ 10,000. The total number of consumers is fixed to $n_A^0=n_A+n_{\left[AR\right]}=200$.

Figure 4

Plot of the per capita feeding rate of the stochastic process defined by the reactions (80)–(83). Simulations were carried out using the Gillespie algorithm with 15,000 steps, while the rates (black dots) were calculated, after a transient of 7500 steps, for different values of consumers concentrations, and compared with the functional response given by Equation (91) (red line). The simulation parameters are $\beta =1.5$, ${\delta }_A=1$, $\alpha =2.5$, $\nu =1$, $\eta =1$, $\chi =100$, and $N=$ 10,000. The total number of resources is fixed to $n_R^0=5000$.