Numerical Methods in Studies of Liquid Crystal Elastomers

Abstract

Liquid crystal elastomers (LCEs) are a type of material with specific features of polymers and of liquid crystals. They exhibit interesting behaviors, i.e., they are able to change their physical properties when met with external stimuli, including heat, light, electric, and magnetic fields. This behavior makes LCEs a suitable candidate for a variety of applications, including, but not limited to, artificial muscles, optical devices, microscopy and imaging systems, biosensor devices, and optimization of solar energy collectors. Due to the wide range of applicability, numerical models are needed not only to further our understanding of the underlining mechanics governing LCE behavior, but also to enable the predictive modeling of their behavior under different circumstances for different applications. Given that several mainstream methods are used for LCE modeling, viz. finite element method, Monte Carlo and molecular dynamics, and the growing interest and reliance on computer modeling for predicting the opto-mechanical behavior of complex structures in real world applications, there is a need to gain a better understanding regarding their strengths and weaknesses so that the best method can be utilized for the specific application at hand. Therefore, this investigation aims to not only to present a multitude of examples on numerical studies conducted on LCEs, but also attempts at offering a concise categorization of different methods based on the desired application to act as a guide for current and future research in this field.

Keywords: Monte Carlo method; finite element method; liquid crystal elastomer; molecular dynamics method; numerical methods.

Figure 1

Stripes at the threshold strain of sample, with the final cross-linking done in the isotropic phase, as seen under the crossed polarized microscope. The orientation of crossed polars is indicated and the length of white lines corresponds to 10μm. Initial director orientation was in the vertical direction, and stretching was performed in the horizontal direction. Close to the transition (just below 77.4 °C) a very fine director modulation can be seen. (a) T = 70.0 °C, (b) T = 75.0 °C, (c) T = 77.0 °C, (d) T = 77.3 °C, (e) T = 77.4 °C [37] (Reprinted with permission from [37]).

Figure 2

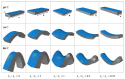
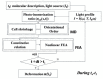
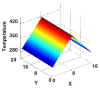
(a) [40], shows the correlation between r = ${\left(\frac{L}{L_{ISO}}\right)}^3$ and T °C, and how it depends on the nematic order parameter. Note that L denotes the length of a sample when it is in the nematic phase and LISO denotes the sample’s reference length, when it is 12 °C above threshold temperature of 78 °C. (b) shows the good agreement between numerical results and experimental data close to the transition temperature [39]. DT accounts for the random fluctuations added to the threshold temperature, which fluctuates specially (Reprinted with permission from [39,40]).

Figure 3

(a,b) Compare experimental data numerical results, obtained from a stretching experiment, are shown in (a,b), respectively [39]. The stretching direction was horizontal (Reprinted with permission from [39]).

Figure 4

(a–d), show the deformation, distribution of stress, and contact pressure of the LCE microvalve, at various temperatures. Note that the color intensity represents the intensity of the local stress distribution. (e) illustrates both the contact region and contact pressure between the LCE valve and surrounding silicon wall. Note that the temperature is close to phase transition temperature [25]. Here, X is the distance measured from the central point of the contact and D is the length of the contact area of the LCE beam [25] (Reprinted with permission from [25]).

Figure 5

Buckling phase diagram of LCE–PS bilayers with different aspect ratios and temperatures, ranging from 30 °C (reference temperature) 80 °C (Reprinted with permission from [25]).

Figure 6

(a) Schematic view of LCE capillary fabrication via PI spin-coating, LC cell assembling, alignment layer rubbing, LCE precursor filling and photo-induced polymerization/crosslinking [43]. (b,c) photographic images of as-prepared LCE capillary with dimensions (Length = 27 mm, Diameter = 0.9 mm and wall thickness = 70 µm); (d) chemical structure of the monomer, crosslinking agent and photoinitiator; (e)chemical structure of polyamic acidused for preparing polyimide alignment layer (Reprinted with permission from [43]).

Figure 7

(a–c) illustrate the case studies considered in this study [26] (Reprinted with permission from [26]). (a) FE simulations carried out on an azo-doped nematic elastomer beam which has been anchored by its right edge. When the beam is exposed to light, it automatically bends in an upward. The purpose of this simulation was to numerically investigate an experiment carried out by Camacho-Lopez et al. [57]. Far left: the beam is shown to be completely in the nematic state. Before exposure, the director is oriented horizontally. Middle: a rapid upward bend is induced by the top (red) layer when it switches to isotropic state. Right: six nematic elastomer actuators (illustrated in blue and green) arrayed in a ring at the tube’s base, cause the formation of a red rubber tube. (b) FE simulations—Left: peristaltic motion a nematic elastomer tube. The motion is caused by periodic modulation of the scalar nematic order parameter along the tube’s length, e.g., by temperature or light. Note that The FE mesh nodes are represented as spheres. Right: peristaltic motion in a thin film, which is designed for covering and transporting the contents of a rigid. (c) FE simulations—A nematic elastomer, mimics the crawling motion of an earthworm.

Figure 8

Outline of the design and experiment process outlined in [60] (Reprinted with permission from [57]).

Figure 9

(a,b) illustrate the regular and irregular samples considered by [88]. (c–f) show the isotropic, nematic (less swelling), nematic (more swelling) and smectic phases, respectively (Reprinted with permission from [88]).

Figure 10

(a,b) represent both cylindrical and spherical domains. (c) shows how the discrete Hamiltonian is defined on each tetrahedron [90] (Reprinted with permission from [90]).

Figure 11

Results showing the configuration of LCEs, having rigid cross-linkers, at different stages, during a simulation where the strain-rate is kept constant. (a) Initial state, showing a clear polydomain structure. (b) Alignment begins after applying strain. (c) As the strain is further increased, only small misaligned clusters remain [8] (Reprinted with permission from [8]).

Figure 12

Workflow of the multiscale model. At an instance in time (t), a photoisomerization ratio is calculated for given values of light intensity (I_o) and temperature (T); and then is used for carrying out MD simulations, which in turn will provide microscopic information to the nonlinear FEA [103] (Reprinted with permission from [103]).

Figure 13

Schematic of the coarse-grained LCP model proposed by [107] (Reprinted with permission from [107]).

Figure 14

The shape evolution of the LCE when inhomogeneous temperature distribution is applied. (a) the LCE is in its initial state (b,c) both show two transitional states, and (d) demonstrates the sample after reaching steady state condition. (e–g) illustrate the LCE sample of (d) from three different points of view [112] (Reprinted with permission from [112]).

Figure 15

Evolution of the LCE sample as a result of inhomogeneous temperature distribution. (a) the LCE is in its initial state (b,c) both show two transitional states, and (d) demonstrates the sample after reaching steady state condition. (e–g) illustrate the LCE sample of (d) from three different points of view [112]. (Reprinted with permission from [112]).

Figure 16

Temperature distribution applied to the sample in Figure 15 [111] (Reprinted with permission from [111]).