Indentation Modulus, Indentation Work and Creep of Metals and Alloys at the Macro-Scale Level: Experimental Insights into the Use of a Primary Vickers Hardness Standard Machine

Abstract

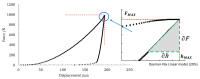
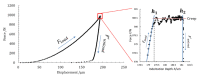
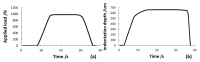
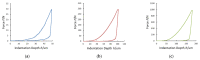
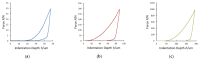
In this work, the experimental method and the calculation model for the determination of indentation moduli, indentation work, and indentation creep of metallic materials, by means of macroscale-level forces provided by a primary hardness standard machine at the National Institute of Metrological Research (INRIM) at the at room temperature were described. Indentation moduli were accurately determined from measurements of indentation load, displacement, contact stiffness and hardness indentation imaging and from the slope of the indentation unloading curve by applying the Doerner-Nix linear model; indentation work, representing the mechanical work spent during the force application of the indentation procedure, was determined by calculating the areas under the loading-unloading indentation curve, through fitting experimental data with a polynomial law. Measurements were performed with a pyramidal indenter (Vickers test). The applied force was provided by a deadweight machine, and the related displacement was measured by a laser interferometric system. Applied forces and the occurring indentation depths were simultaneously measured: the resulting loading-unloading indentation curve was achieved. Illustrative tests were performed on metals and alloy samples. Discussion and comments on the suitability of the proposed method and analysis were reported.

Keywords: Vickers hardness test; indentation hardness; indentation modulus; indentation work.

Figure 1

Experimental measuring systems used in this investigation: primary hardness standard deadweight machine with the details of the anvil and the interferometric system.

Figure 2

Loading–unloading paths of the indentation curve, expressed as a function of applied force and displacement, with quantities used for the determination of contact stiffness S.

Figure 3

Loading–unloading paths of the indentation curve, expressed as a function of applied force and displacement with the indication of the creep of the material during the application of a constant force.

Figure 4

Experimental areas representing the plastic and elastic parts of the indentation work, under the loading and unloading indentation curves.

Figure 5

Series of loading and unloading cycles of the indentation curve at a single point (a); and the linear regression of the last reversed unloading curve for the HV100 procedure (b).

Figure 6

Experimental data of the applied load (a) and the indenter displacement (approaching and indentation) (b) of a HV100 indentation test. Forces were applied at a rate of 160 N/s (load displacement speed: 100 µm/s). The maximum load was applied for 15 s.

Figure 7

Loading–unloading curves of the Vickers hardness (HV) tests on stainless steel: (a) HV3; (b) HV30; (c) HV100.

Figure 8

Loading–unloading curves of the HV tests on aluminum alloy: (a) HV3; (b) HV30; (c) HV100.

Figure 9

Loading-unloading curves of the HV tests on copper alloy: (a) HV3; (b) HV30; (c) HV100.

Figure 10

Loading–unloading curves of the HV tests on Cu–Cr–Zr alloy: (a) HV3; (b) HV30; (c) HV100.

Figure 11

(a) Loading curve obtained by Equation (12); (b) best fit (red) of the unloading curve obtained by Equation (13) and the identification of the expected permanent indentation depth h_p from the zero value of the fitting curve.

Figure 12

Schematic representation of the plastic, elastic, and creep parts of the indentation work beneath the loading and unloading indentation curves as a function of applied force and displacement.