The energy-spectrum of bicompatible sequences

Abstract

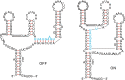
Background: Genotype-phenotype maps provide a meaningful filtration of sequence space and RNA secondary structures are particular such phenotypes. Compatible sequences, which satisfy the base-pairing constraints of a given RNA structure, play an important role in the context of neutral evolution. Sequences that are simultaneously compatible with two given structures (bicompatible sequences), are beacons in phenotypic transitions, induced by erroneously replicating populations of RNA sequences. RNA riboswitches, which are capable of expressing two distinct secondary structures without changing the underlying sequence, are one example of bicompatible sequences in living organisms.

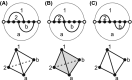
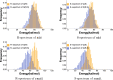
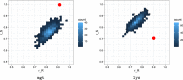
Results: We present a full loop energy model Boltzmann sampler of bicompatible sequences for pairs of structures. The sequence sampler employs a dynamic programming routine whose time complexity is polynomial when assuming the maximum number of exposed vertices, [Formula: see text], is a constant. The parameter [Formula: see text] depends on the two structures and can be very large. We introduce a novel topological framework encapsulating the relations between loops that sheds light on the understanding of [Formula: see text]. Based on this framework, we give an algorithm to sample sequences with minimum [Formula: see text] on a particular topologically classified case as well as giving hints to the solution in the other cases. As a result, we utilize our sequence sampler to study some established riboswitches.

Conclusion: Our analysis of riboswitch sequences shows that a pair of structures needs to satisfy key properties in order to facilitate phenotypic transitions and that pairs of random structures are unlikely to do so. Our analysis observes a distinct signature of riboswitch sequences, suggesting a new criterion for identifying native sequences and sequences subjected to evolutionary pressure. Our free software is available at: https://github.com/FenixHuang667/Bifold .

Keywords: Evolutionary transition; Riboswitch; Topological nerve.

Fig. 1

Riboswitch. Alternative structures of the Adenine riboswitch [24] and its switching sequence (blue), involved two respective helices

Fig. 2

From two secondary structures to a topological space: A two secondary structures drawn in the upper- and lower-half plan respectively. A rainbow arc (0, 9) is added to both of the structures to close to exterior loop. B The secondary structures are decomposed into loops. The loops induce a hyper-graph $G=(V=\{0,\dots ,9\},E)$, where $E=\{e_1,e_2,e_3,e_4,e_5,e_6\}$ with $e_1=\{0,1,4,5,7,8,9\},e_2=\{1,2,3,4\},e_3=\{2,3\},e_4=\{5,6,7\}$, $e_5=\{0,1,2,3,4,5,6,8,9\}$ and $e_6=\{6,7,8\}$ are loops. C The nerve over E. A $(d-1)$-simplex represent the nontrivial intersection of d loops. D The topological quotient space K(R) induced by C, where a ribbon induced by $\{e_1,e_2,e_5,e_3\}$ is glued to a sphere induced by $\{e_1,e_5,e_4,e_6\}$

Fig. 3

Geometric interpretation of the 0th-, 1st-, and 2nd- homology group. A The rank of the 0th homology group is 2, counting the number of connected components, where each of them can be contracted to a single point. B The rank of the 1st homology group is 2, counting the number of uncontactable circles on a torus. C The rank of the 2nd homology group is 2, counting the number of empty volume (2-dimensional holes) induced by the spheres

Fig. 4

A An RNA secondary structure. B Diagram representation of A. C A secondary structure with a rainbow arc (dash). D Loops in a secondary structure. The loop (gray) contains a distinguished maximal arc (1, 17). E A bistructure B is a collection of loops $\{L_1,\dots ,L_9\}$. $X=\{L_3,L_7,L_9\}$ (blue) is an irreducible substructure of B with its complement $\overline{X}=\{L_1,L_2,L_4,L_5,L_6,L_8\}$. We mark the exposed vertices $E^X=V^X\cap V^{\overline{X}}$ in red. The closure of X is given by $\tilde{X}=\{L_2,L_3,L_4,L_6,L_7,L_8,L_9\}$

Fig. 5

Illustration of the recursion for the partition function. Given a bistructure X with exposed vertices $v_1$ and $v_2$, we decomposed X into a loop $L(v_1,u_1,u_2,u_3)$ and a substructure $X^{\prime }(v_1,u_1,u_2,u_3,v_2)$. Here we assume $v_1$, $u_1$, $u_2$, $u_3$, and $v_2$ are contained in loops of $X^{\prime }$, hence $v_1$ and $v_2$ remain exposed and $u_1$, $u_2$, and $u_3$ are newly exposed vertices

Fig. 6

A decomposition of a bistructure (LHS) and the evolution of its loop nerve (RHS). LHS: exposed vertices are labelled red. RHS: the loops 1, 2, 3, 5 and 6 form a sphere. Removing one loop from this sphere is tantamount to deleting one vertex of the loop nerve. The white vertices in the loop nerve represent the boundary of the substructure. The sphere corresponding to the crossing component is resolved by removing the S-arc

Fig. 7

Examples of topological realizations of the loop nerves for different bistructures: A an empty tetrahedron or a sphere), B a filled tetrahedron, and C two filled triangles glued along a mutual edge

Fig. 8

Splitting an overlap without inducing crossing arcs (A). The split is tantamount to removing an edge of the corresponding filled tetrahedron as well as its interior, ending up with two triangles that are still glued along the opposite edge from the edge we removed. B The split effect on the corresponding simplicial complex of A

Fig. 9

A bistructure having no overlap and crossing arcs (left), its loop nerve (middle), and the $\ast$-graph (right). Each vertex in the $\ast$-graph presents a triangle in the loop nerve, labeled by a triple of loops. Its $\ast$-graph is a tree

Fig. 10

Topologically guided optimal tree decomposition: A a bistructure without crossing arcs or overlaps. B The hyper-graph of A. C Its quotient space is a ribbon. D The optimal tree decomposition of B obtained by following (C)

Fig. 11

The R- and S spectra of the riboswitch structure pair, add and rand1. Top left: $f_{Q(R)}^R$ versus $f_{{Q(R)|}_S}^R$ for add. Top right: $f_{Q(S)}^S$ versus $f_{{Q(S)|}_R}^S$ for add. Bottom left: $f_{Q(R)}^R$ versus $f_{{Q(R)|}_S}^R$ for rand1. Bottom right: $f_{Q(S)}^S$ versus $f_{{Q(S)|}_R}^S$ for rand1

Fig. 12

The R- and S spectra of the riboswitch structure pair, add and rand1. Top left: $f_{Q(R)}^R$ versus $f_{Q(R,S)}^R$ for add. Top right: $f_{Q(S)}^S$ versus $f_{Q(R,S)}^S$ for add. Bottom left: $f_{Q(R)}^R$ versus $f_{Q(R,S)}^R$ for rand1. Bottom right: $f_{Q(S)}^S$ versus $f_{Q(R,S)}^S$ for rand1

Fig. 13

$(r_R,r_S)$ for the riboswitches mgt (left) and lys (right): Boltzmann sampled sequences versus native sequences. For each riboswitch we Boltzmann sample ${10}^3$ sequences and compute $(r_R,r_S)$ for the sampled sequences (blue). We contrast this with $(r_R,r_S)$ of for the respective, native riboswitch sequence (red)

Fig. 14

The energy weighed space of bicompatible sequences. $(w_R,w_S)$ of the six riboswitch structure pairs, presented in Table 1 (blue). Furthermore: $(w_R,w_S)$ of 50 random structure pairs of length 150, as control set (red)