Roton-like acoustical dispersion relations in 3D metamaterials

Abstract

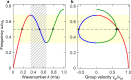
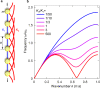
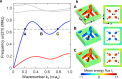
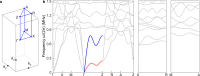
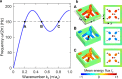
Roton dispersion relations have been restricted to correlated quantum systems at low temperatures, such as liquid Helium-4, thin films of Helium-3, and Bose-Einstein condensates. This unusual kind of dispersion relation provides broadband acoustical backward waves, connected to energy flow vortices due to a "return flow", in the words of Feynman, and three different coexisting acoustical modes with the same polarization at one frequency. By building mechanisms into the unit cells of artificial materials, metamaterials allow for molding the flow of waves. So far, researchers have exploited mechanisms based on various types of local resonances, Bragg resonances, spatial and temporal symmetry breaking, topology, and nonlinearities. Here, we introduce beyond-nearest-neighbor interactions as a mechanism in elastic and airborne acoustical metamaterials. For a third-nearest-neighbor interaction that is sufficiently strong compared to the nearest-neighbor interaction, this mechanism allows us to engineer roton-like acoustical dispersion relations under ambient conditions.

Fig. 1. Roton-like acoustical wave dispersion relation.

a The acoustical wave’s angular frequency $\omega \left(k\right)$ is depicted versus wavenumber $k$. The dispersion relation starts off with the usual linear increase of $\omega$ versus $k$. At a finite characteristic wavenumber, the dispersion relation exhibits a parabolic minimum. In a certain frequency range (highlighted by the light-yellow background), a single frequency $\omega$ leads to three modes at different $k$ (exemplified by the dashed line and the black dots), hence different wavelengths $\lambda =2\pi /k$. In the hatched wavenumber interval, the group velocity $v_{\mathrm{gr}}=\mathrm{d}\omega /\mathrm{d}k$ is negative, whereas the phase velocity $v_{\mathrm{ph}}=\omega /k$ is positive. In a crystal with period $a$, the edges of the first Brillouin zone at wavenumbers $\pm \pi /a$ are important. b Corresponding group velocity versus angular frequency $\omega$, normalized by the phase velocity in the long-wavelength limit, $k\to 0$. The different colors serve to connect the different parts of the dispersion relation between a and b. Panels a and b can be taken as schemes. They actually correspond to solutions of the 1D toy model (cf. Fig. 2b) with parameters $N=3$, $K_N/K_1=3$, and ${\omega }_0=\sqrt{\left(K_1+K_N{N}^2\right)/m}$.

Fig. 2. One-dimensional toy model.

a Masses $m$ (yellow dots) are connected to their nearest neighbors separated by distance $a$ by Hooke’s springs with spring constants $K_1$ (blue straight lines). In addition, all masses are connected to their $N$th-nearest neighbors at distance $Na$ by springs with Hooke’s spring constants $K_N$ (red curved lines). As an example, we choose $N=3$. For $K_1\ne 0$, the spatial period of this arrangement is $a$. Hence, the first Brillouin zone is given by wavenumber $∣k∣\le \pi /a$. b Dispersion relation $\omega \left(k\right)=\omega \left(-k\right)$. The differently colored curves (see legend) represent different ratios of the spring constants $K_3/K_1$, increasing from top to bottom. For clarity, we fix the phase velocity in the long-wavelength limit $k\to 0$, i.e., $v_{\mathrm{ph}}=a\sqrt{\left(K_1+K_N{N}^2\right)/m}=\mathrm{const}=a{\omega }_0$.

Fig. 3. Designed three-dimensional elastic metamaterial structure.

a The architecture incorporates nearest-neighbor as well as beyond-nearest-neighbor interactions (cf. Fig. 2a) and is composed of a single ordinary linearly elastic constituent material. The colors are for illustration only. Elements mediating the elastic interaction between one layer and its third-nearest-neighbor along the $z$-direction are highlighted in red. The blue and red cylindrical rods have a radius of $r_1/a_z=0.08$ and $r_2/a_z=0.12$, respectively. The structure has no center of inversion but two mirror planes and a rotation-reflection symmetry, making it achiral and leading to a degeneracy of the lowest two transverse acoustical bands (cf. Fig. 4). The period of the structure along the $z$-direction is $a_z$, the corresponding first Brillouin zone edges lye at wavenumbers $k_z=\pm \pi /a_z$ (cf. Fig. 4). The period or lattice constant along the $x$- and $y$-directions is $a_{xy}=2a_z$. The other geometrical parameters are $t_1/a_z=0.40$, $t_2/a_z=0.60$, and $a_z=100\mathrm{\mu }\mathrm{m}$. b $3\times 3\times 5$ unit cells out of a corresponding bulk metamaterial, with the front corner cut out to allow for a view inside. The part highlighted in red illustrates the beyond-nearest-neighbor interaction. Two red rods connect a first cube to the red frame (made partly transparent at the corner). Two further red rods connect this frame to a second cube, which has a distance $3a_z$ with respect to the first cube. An animated view of the structure is given in Supplementary Movie 1.

Fig. 4. Elastic metamaterial phonon band structure along z-direction.

a The dispersion relation $\omega \left(k_z\right)=\omega \left({-k}_z\right)$ of the architecture in Fig. 3 is shown for propagation of elastic waves along the $z$-direction with wavenumber $k_z$. The spatial period is $a_z$, corresponding to the first Brillouin zone given by the condition $∣k_z∣\le \pi /a_z$ (cf. Fig. 1). The two transverse acoustical bands, which are degenerate by symmetry, are plotted in red, the single longitudinal acoustical band in blue. Higher dispersion branches are of lesser importance here and are depicted in gray. They partly result from local resonances within the unit cell, leading to finite values of $\omega$ at zero wavenumber $k_z=0$. b Mean energy flux $I_z$ along the $z$-direction (on a false-color scale) corresponding to three eigenmodes marked as A, B, and C of the longitudinal band for the same frequency $0.65\mathrm{MHz}$. The left column shows an oblique view of the unit cell, the right column a cut through the $xy$-plane. The mean energy flux in the thin vertical rods in the middle is positive for all three modes. The same holds true for the mean energy flow through the thicker oblique rods for modes A and C. The oblique rods mediate the beyond-nearest-neighbor interactions. In contrast, the energy flux through the oblique rods for mode B is negative, indicating a backward-wave behavior. Integration of the energy flux over the $xy$-plane for this mode also leads to a negative total energy flow, consistent with a negative group velocity. Parameters are $a_z=100\mathrm{\mu m}$ (cf. Fig. 3), aspect ratios as given in Fig. 3, Young’s modulus $E=4.2\mathrm{GPa}$, Poisson’s ratio $\nu =0.4$, and mass density ρ = 1140 kg m⁻³ for the constituent material.

Fig. 5. Elastic metamaterial phonon band structure in 3D.

As Fig. 4 (for the metamaterial structure shown in Fig. 3), but for many high-symmetry directions rather than only the $\mathrm{\Gamma }Z$ or $z$-direction as in Fig. 4. a Illustration of the first Brillouin zone of the tetragonal-symmetry real-space lattice and selected high-symmetric directions in reciprocal space (marked in blue). b Calculated three-dimensional phonon band structure with the characteristic directions as indicated in a. Clearly, due to the used tetragonal symmetry, roton-like acoustical dispersion relations only occur for the $\mathrm{\Gamma }Z$ direction. The corresponding colored bands (blue and red) are the same as the ones shown in Fig. 4.

Fig. 6. Roton-like behavior for airborne sound.

We consider a structure which is the complement of the one shown in Fig. 3. This leads to a network of channels inside a rigid material in which air can flow. a Acoustical dispersion relation $\omega \left(k_z\right)=\omega \left(-k_z\right)$ for air pressure waves propagating along the $z$-direction, exhibiting a roton-like minimum within the first Brillouin zone $∣k_z∣\le \pi /a_z$. Higher bands at (much) higher frequencies are not shown. b Mean energy flux $I_z$ on a false-color scale along the $z$-direction for the three eigenmodes A, B, and C marked in a at the same frequency of $150\mathrm{Hz}$. As in Fig. 4b, backward-wave behavior is observed for mode B, for which the group velocity is negative. The lattice constant is chosen as $a_z=10\mathrm{cm}$. All other parameter ratios are the same as in Fig. 3. We assume ambient conditions, corresponding to an airborne speed of sound of $v_{\mathrm{air}}=340\mathrm{m}/\mathrm{s}$ and a mass density of ${\rho }_{\mathrm{air}}=1.29\mathrm{kg}{\mathrm{m}}^{-3}$.