Subspace-constrained approaches to low-rank fMRI acceleration

Abstract

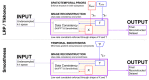
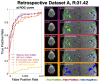
Acceleration methods in fMRI aim to reconstruct high fidelity images from under-sampled k-space, allowing fMRI datasets to achieve higher temporal resolution, reduced physiological noise aliasing, and increased statistical degrees of freedom. While low levels of acceleration are typically part of standard fMRI protocols through parallel imaging, there exists the potential for approaches that allow much greater acceleration. One such existing approach is k-t FASTER, which exploits the inherent low-rank nature of fMRI. In this paper, we present a reformulated version of k-t FASTER which includes additional L2 constraints within a low-rank framework. We evaluated the effect of three different constraints against existing low-rank approaches to fMRI reconstruction: Tikhonov constraints, low-resolution priors, and temporal subspace smoothness. The different approaches are separately tested for robustness to under-sampling and thermal noise levels, in both retrospectively and prospectively-undersampled finger-tapping task fMRI data. Reconstruction quality is evaluated by accurate reconstruction of low-rank subspaces and activation maps. The use of L2 constraints was found to achieve consistently improved results, producing high fidelity reconstructions of statistical parameter maps at higher acceleration factors and lower SNR values than existing methods, but at a cost of longer computation time. In particular, the Tikhonov constraint proved very robust across all tested datasets, and the temporal subspace smoothness constraint provided the best reconstruction scores in the prospectively-undersampled dataset. These results demonstrate that regularized low-rank reconstruction of fMRI data can recover functional information at high acceleration factors without the use of any model-based spatial constraints.

Keywords: Acceleration; Low Rank; Low Resolution Priors; Temporal Resolution; Temporal Smoothing; Tikhonov Regularization; fMRI; k-t FASTER.

Fig. 1

A schematic overview of a reconstruction via various constrained-subspace approaches. For the LRP, X_prior and T_prior are created using a windowed version of the under-sampled data according to only the rank constraints and coil sensitivity information. For Tikhonov, X_prior and T_prior are zero-filled. X_prior and T_prior are fed as a constraint into the final reconstruction, combining with the data consistency term on an unwindowed dataset to produce the final output. The temporal subspace smoothness schematic shows a finite difference matrix ∇ applied solely to the temporal component matrix T, before also being combined with the data consistency term.

Fig. 2

A demonstration of the flexibility of a golden angle sampling scheme, and of the k-space windowing required to create LRP constraints. EPI planes (left) are rotated by ≈ 111.25° around the phase-encoding axis. These rotated planes can then be flexibly combined. If many planes are used (top, blue) then a clean image is easily generated, but at the cost of temporal resolution. If fewer planes are used (middle, yellow) then more images are generated per second, but with an increased number of artefacts. The central part of under-sampled k-space satisfies the Nyquist criterion, even if the full extent of the under-sampled k-space does not. By windowing this central k-space (green, bottom), an accurate low-resolution depiction of the underlying data can be created.

Fig. 3

The canonical correlation scores (CCS) of retrospective dataset A vs a ground truth for a): Tikhonov-constrained reconstructions, b): LRP-constrained reconstructions, c): Temporal Subspace Smoothness reconstructions. X CCS and T CCS refer to the spatial and temporal Canonical Correlation Scores respectively. The acceleration factors shown are: R = 15.71 (10 blades/frame), R = 31.42 (5 blades/frame), R = 39.27 (4 blades/frame), and R = 52.36 (3 blades/frame). The λ values encoding the pre-existing k-t FASTER and k-t PSF methods are shown on the right for each constraint.

Fig. 4

R = 31.42 (5 blades/frame) retrospective dataset A reconstructions. a) ROC curves, legend lists full curve AUC. b)-f) Activation maps using a z-statistic corresponding to an FPR of 0.15%. g)-k) A medial zoom of the associated activation maps. b/g) Tikhonov: λ_X = 10⁻⁵, λ_T = 10⁻⁵, c/h) LRP: λ_X = 10⁻⁵, λ_T = 10⁻⁵, d/i) Temporal subspace smoothness: λ _∇ = 10⁻⁵, e/j) k-t FASTER, f/k) k-t PSF. Maps b)-k) use green true positive pixels, red false positives, and blue false negatives.

Fig. 5

R = 52.36 (3 blades/frame) retrospective dataset A reconstructions. a) ROC curves, legend lists full curve AUC. b)-f) Activation maps using a z-statistic corresponding to an FPR of 0.15%. g)-k) A medial zoom of the associated activation maps. b/g) Tikhonov: λ_X = 10⁻⁵, λ_T = 10⁻⁵, c/h) LRP: λ_X = 10⁻⁴, λ_T = 10⁻⁶, d/i) Temporal subspace smoothness: λ _∇= 10⁻⁴, e/j) k-t FASTER, f/k) k-t PSF. Maps b)-k) use green true positive pixels, red false positives, and blue false negatives.

Fig. 6

6a: Retrospective dataset B reconstruction AUC results. Each bar represents the mean AUC of five different instantiations of Gaussian noise in k-t space at a specific SNR for a specific reconstruction method, except for the lefthand set, which represent a single noiseless reconstruction. The error bars show the range of AUC values. 6b: An example activation map at each noise value for each reconstruction method. See Supplementary Figs. 3–5 for the full set of activation maps and the individual ROC curves. As with Figs. 4-5, green pixels represent true positives, red pixels represent false positives, blue pixels represent false negatives. The z-statistics threshold yielded a false positive rate of 0.15%.

Fig. 7

The ROC curves across eight slices for a) R = 7.85 (20 blades/frame), b) R = 15.71 (10 blades/frame), and c) R = 26.18 (6 blades/frame). The ground truth is the long dataset taken under similar experimental conditions, at a threshold of z ≥ 4.8. The false-positive rate is shown on the x-axis up to 0.02, in order to allow visualization of the analytically relevant representation of the activation maps.

Fig. 8

Prospective Dataset A, R = 26.18. The activation maps for every second slice of the reconstruction, at a threshold defined by a 0.15% volumetric false positive rate. Supplementary Fig. 8 shows the activation maps of all slices.

Fig. 9

The ROC curves for each different slice of Prospective Dataset B at R = 26.18 (6 blades/frame), compared to an R = 7.85 k-t FASTER reconstruction of the same slice thresholded at either z ≥ 4.0 (Motor 1/Visual 1) or z ≥ 2.7 (Motor 2/Visual 2). The false-positive rate is shown on the x-axis up to 0.02, in order to allow visualization of the analytically relevant representation of the activation maps.

Fig. 10

Prospective Dataset B, R = 26.18. The activation maps for each reconstruction, at a threshold defined by a 0.15% volumetric false positive rate. The background brain is the mean temporal image for that reconstruction.