Evolution of dominance in gene expression pattern associated with phenotypic robustness

Abstract

Background: Mendelian inheritance is a fundamental law of genetics. When we consider two genomes in a diploid cell, a heterozygote's phenotype is dominated by a particular homozygote according to the law of dominance. Classical Mendelian dominance is concerned with which proteins are dominant, and is usually based on simple genotype-phenotype relationship in which one gene regulates one phenotype. However, in reality, some interactions between genes can exist, resulting in deviations from Mendelian dominance. Whether and how Mendelian dominance is generalized to the phenotypes of gene expression determined by gene regulatory networks (GRNs) remains elusive.

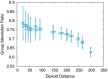
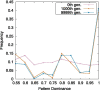
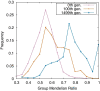
Results: Here, by using the numerical evolution of diploid GRNs, we discuss whether the dominance of phenotype evolves beyond the classical Mendelian case of one-to-one genotype-phenotype relationship. We examine whether complex genotype-phenotype relationship can achieve Mendelian dominance at the expression level by a pair of haplotypes through the evolution of the GRN with interacting genes. This dominance is defined via a pair of haplotypes that differ from each other but have a common phenotype given by the expression of target genes. We numerically evolve the GRN model for a diploid case, in which two GRN matrices are added to give gene expression dynamics and simulate evolution with meiosis and recombination. Our results reveal that group Mendelian dominance evolves even under complex genotype-phenotype relationship. Calculating the degree of dominance shows that it increases through the evolution, correlating closely with the decrease in phenotypic fluctuations and the increase in robustness to initial noise. We also demonstrate that the dominance of gene expression patterns evolves concurrently. This evolution of group Mendelian dominance and pattern dominance is associated with phenotypic robustness against meiosis-induced genome mixing, whereas sexual recombination arising from the mixing of genomes from the parents further enhances dominance and robustness. Due to this dominance, the robustness to genetic differences increases, while optimal fitness is sustained to a significant difference between the two genomes.

Conclusion: Group Mendelian dominance and gene-expression pattern dominance are achieved associated with the increase in phenotypic robustness to noise.

Keywords: Diploid; Evolution; Gene regulatory network; Mendelian dominance; Robustness; Theoretical model.

Fig. 1

Fitness as a function of evolutional generation for the asexual (black line), MR (blue line), and MO (green line) modes. The mutation rate per edge = $4\times {10}^{-4}$ and the strength of noise = 0. The increase in fitness was saturated within 2000 generations. The average of over 50 samples is plotted. The error bar represents the standard deviation (SD) over them

Fig. 2

Mutation rate dependence of the average fitness. The average fitness was computed for 100 individuals representing the last generation in the evolution of over 10,000 generations for the asexual (black circles), MR (blue triangles), and MO (green diamonds) modes. The noise amplitude $\sigma$ was 0.0. For increasing mutation rates, error catastrophe occurs, which prevents the average fitness from rising through evolution over 10,000 generations. The recombination-only reference case is also plotted (orange triangles). The average over 50 samples is plotted. The error bar represents the SD over them

Fig. 3

Frequency of group Mendelian ratio (GMR) in the 0th, 100th, and 1499th generation. This frequency is calculated by each focused gene in 30 samples. GMR is increased along the evolution and over 10% of them reach complete GMD. The mutation rate per edge = ${10}^{-4}$ and the strength of noise = ${10}^{-4}$. This frequency is measured in MR mode. The bin is 0.05

Fig. 4

GMR as a function of mutation rate. The GMR at the ${10}^4$-th generation is shown for the asexual (black dots), MR (blue triangles), and MO (green diamonds) modes. The noise amplitude was 0.0. Data for the RO reference case are also plotted (orange triangles). The average over 50 samples is plotted. The error bar represents the SD over them

Fig. 5

Correlation between the GMR, average fitness, and SD of the fitness. Each variable was computed as the value of the ${10}^4$-th generation for the MR case. The points were obtained across different mutation rates from $2\times {10}^{-4}$ to $2\times {10}^{-2}$, as indicated by the color of the data, while the noise level satisfied $0.0\le \sigma \le 0.1$. a GMR as a function of the average fitness, b GMR as a function of the SD of the fitness, c SD of the fitness as a function of the average fitness. Note that aand ceach have three branches corresponding to different noise levels, whereas (b) does not, implying that the GMR is dominantly correlated with the fluctuation of the fitness rather than its average. The average over 50 samples is plotted. The error bar represents the SD over them. Correlation coefficient is (a) 0.952, b $-0.973$, c $-0.926$

Fig. 6

GMR plotted against the isogenetic SD of fitness due to initial noise, i.e., perturbation to the initial conditions. The GMR was computed following the same procedure as in Fig. 5, for the MR case, whereas the fitness variance was computed by distributing the initial condition for $x_i$ with the variance $\sigma$, which is either ${10}^{-2}$ or ${10}^{-1}$. The data correspond to the equivalent mutation rates as used in Fig. 5. The average over 50 samples is plotted. The error bar denotes the SD over them

Fig. 7

GMR as a function of the distance between the two genomes. The distance was computed as the Euclidean distance between the matrix elements in two genomes, $J_{\mathit{ij}}^{(1)}$ and $J_{\mathit{ij}}^{(2)}$. All data were obtained from the evolved GRNs for the MR case shown in Fig. 5. We simulated GRNs with 20 genes, such that the number of matrix elements, that is, the maximal Hamming distance (i.e., the number of different elements), is $20\times 20=400$. Consequently, the GMR (and the fitness) maintains a high value until half the elements have been changed. The average over 50 samples is plotted. The error bar represents the SD over them

Fig. 8

Increase in pattern dominance and evolution. Frequency of pattern dominance in the 0th, 1000th, and 9999th generation. For each generation, this frequency is computed over ten samples. Pattern dominance is increased along with the evolution, and over 50% of heterozygotes reach complete pattern dominance. The mutation rate per edge = ${10}^{-4}$ and the strength of noise = ${10}^{-4}$. This frequency is measured in the MR mode. The bin is 0.05

Fig. 9

Increase in GMR and the evolution in the case with distinct protein synthesis from each gene. Frequency of GMR in the 0th, 100th, and 1499th generation. This frequency is calculated by each focused gene in 30 samples. GMR is increased along with the evolution, and over 10% of them reached complete GMD. This also supports our results above. The mutation rate per edge = ${10}^{-4}$ and the strength of noise = ${10}^{-4}$. This frequency is measured in the MR mode. The bin is 0.05

Fig. 10

Renaming of haplotypes

Fig. 11

Testing the homozygote and heterozygote cases