Dynamical characterization of antiviral effects in COVID-19
- PMID: 34093069
- PMCID: PMC8162791
- DOI: 10.1016/j.arcontrol.2021.05.001
Dynamical characterization of antiviral effects in COVID-19
Abstract
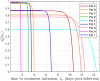
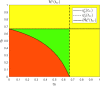
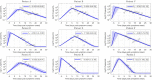
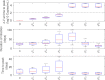
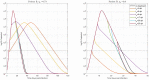
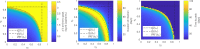
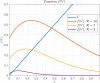
Mathematical models describing SARS-CoV-2 dynamics and the corresponding immune responses in patients with COVID-19 can be critical to evaluate possible clinical outcomes of antiviral treatments. In this work, based on the concept of virus spreadability in the host, antiviral effectiveness thresholds are determined to establish whether or not a treatment will be able to clear the infection. In addition, the virus dynamic in the host - including the time-to-peak and the final monotonically decreasing behavior - is characterized as a function of the time to treatment initiation. Simulation results, based on nine patient data, show the potential clinical benefits of a treatment classification according to patient critical parameters. This study is aimed at paving the way for the different antivirals being developed to tackle SARS-CoV-2.
Keywords: Antiviral effectiveness; Dynamic characterization; In-host model; SARS-CoV-2.
© 2021 Elsevier Ltd. All rights reserved.
Conflict of interest statement
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Figures








Similar articles
-
Characterization of SARS-CoV-2 dynamics in the host.Annu Rev Control. 2020;50:457-468. doi: 10.1016/j.arcontrol.2020.09.008. Epub 2020 Oct 6. Annu Rev Control. 2020. PMID: 33041634 Free PMC article.
-
Antiviral Activity of Type I, II, and III Interferons Counterbalances ACE2 Inducibility and Restricts SARS-CoV-2.mBio. 2020 Sep 10;11(5):e01928-20. doi: 10.1128/mBio.01928-20. mBio. 2020. PMID: 32913009 Free PMC article.
-
Impulsive Neural Control to Schedule Antivirals and Immunomodulators for COVID-19.Proc IEEE Conf Decis Control. 2022 Dec;2022:5633-5638. doi: 10.1109/cdc51059.2022.9992454. Epub 2023 Jan 10. Proc IEEE Conf Decis Control. 2022. PMID: 37051484 Free PMC article.
-
Oral antiviral treatments for COVID-19: opportunities and challenges.Pharmacol Rep. 2022 Dec;74(6):1255-1278. doi: 10.1007/s43440-022-00388-7. Epub 2022 Jul 25. Pharmacol Rep. 2022. PMID: 35871712 Free PMC article. Review.
-
[Umifenovir and coronavirus infections: a review of research results and clinical practice].Ter Arkh. 2020 Dec 26;92(11):91-97. doi: 10.26442/00403660.2020.11.000713. Ter Arkh. 2020. PMID: 33720612 Review. Russian.
Cited by
-
Response of vaccination on community transmission of COVID-19: a dynamical approach.Eur Phys J Spec Top. 2022;231(18-20):3749-3765. doi: 10.1140/epjs/s11734-022-00652-0. Epub 2022 Aug 16. Eur Phys J Spec Top. 2022. PMID: 35991944 Free PMC article.
-
A biomathematical model of SARS-CoV-2 in Syrian hamsters.Sci Rep. 2024 Dec 18;14(1):30541. doi: 10.1038/s41598-024-80498-9. Sci Rep. 2024. PMID: 39695178 Free PMC article.
-
Multi-objective control to schedule therapies for acute viral infections.J Math Biol. 2025 Feb 4;90(2):25. doi: 10.1007/s00285-025-02188-y. J Math Biol. 2025. PMID: 39904788
-
A theory for viral rebound after antiviral treatment: A study case for SARS-CoV-2.Math Biosci. 2025 Jan;379:109339. doi: 10.1016/j.mbs.2024.109339. Epub 2024 Nov 20. Math Biosci. 2025. PMID: 39577689
-
Effectiveness of Antiviral Therapy in Highly-Transmissible Variants of SARS-CoV-2: A Modeling and Simulation Study.Front Pharmacol. 2022 Feb 9;13:816429. doi: 10.3389/fphar.2022.816429. eCollection 2022. Front Pharmacol. 2022. PMID: 35222030 Free PMC article.
References
-
- Callaway D.S., Perelson A.S. HIV-1 infection and low steady state viral loads. Bulletin of Mathematical Biology. 2002;64(1):29–64. - PubMed
LinkOut - more resources
Full Text Sources
Miscellaneous
