Dynamics of Drug Resistance: Optimal Control of an Infectious Disease
- PMID: 34113048
- PMCID: PMC8188892
- DOI: 10.1287/opre.2018.1817
Dynamics of Drug Resistance: Optimal Control of an Infectious Disease
Abstract
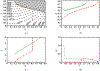
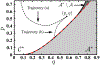
Antimicrobial resistance is a significant public health threat. In the U.S. alone, 2 million people are infected and 23,000 die each year from antibiotic resistant bacterial infections. In many cases, infections are resistant to all but a few remaining drugs. We examine the case where a single drug remains and solve for the optimal treatment policy for an SIS infectious disease model incorporating the effects of drug resistance. The problem is formulated as an optimal control problem with two continuous state variables, the disease prevalence and drug's "quality" (the fraction of infections that are drug-susceptible). The decision maker's objective is to minimize the discounted cost of the disease to society over an infinite horizon. We provide a new generalizable solution approach that allows us to thoroughly characterize the optimal treatment policy analytically. We prove that the optimal treatment policy is a bang-bang policy with a single switching time. The action/inaction regions can be described by a single boundary that is strictly increasing when viewed as a function of drug quality, indicating that when the disease transmission rate is constant, the policy of withholding treatment to preserve the drug for a potentially more serious future outbreak is not optimal. We show that the optimal value function and/or its derivatives are neither C 1 nor Lipschitz continuous suggesting that numerical approaches to this family of dynamic infectious disease models may not be computationally stable. Furthermore, we demonstrate that relaxing the standard assumption of constant disease transmission rate can fundamentally change the shape of the action region, add a singular arc to the optimal control, and make preserving the drug for a serious outbreak optimal. In addition, we apply our framework to the case of antibiotic resistant gonorrhea.
Keywords: antimicrobial resistance; dynamic health policy; health care management; infectious disease models; optimal control.
Figures
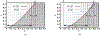
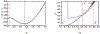

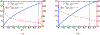

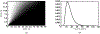
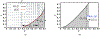
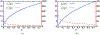

Similar articles
-
Malaria Surveillance - United States, 2016.MMWR Surveill Summ. 2019 May 17;68(5):1-35. doi: 10.15585/mmwr.ss6805a1. MMWR Surveill Summ. 2019. PMID: 31099769
-
Neisseria gonorrhoeae Antimicrobial Susceptibility Surveillance - The Gonococcal Isolate Surveillance Project, 27 Sites, United States, 2014.MMWR Surveill Summ. 2016 Jul 15;65(7):1-19. doi: 10.15585/mmwr.ss6507a1. MMWR Surveill Summ. 2016. PMID: 27414503
-
Optimal Data Injection Attacks in Cyber-Physical Systems.IEEE Trans Cybern. 2018 Dec;48(12):3302-3312. doi: 10.1109/TCYB.2018.2846365. Epub 2018 Jun 26. IEEE Trans Cybern. 2018. PMID: 29994695
-
[Development of antituberculous drugs: current status and future prospects].Kekkaku. 2006 Dec;81(12):753-74. Kekkaku. 2006. PMID: 17240921 Review. Japanese.
-
Quality standard for antimicrobial prophylaxis in surgical procedures. Infectious Diseases Society of America.Clin Infect Dis. 1994 Mar;18(3):422-7. doi: 10.1093/clinids/18.3.422. Clin Infect Dis. 1994. PMID: 8011827 Review.
Cited by
-
Optimal subscription models to pay for antibiotics.Soc Sci Med. 2022 Apr;298:114818. doi: 10.1016/j.socscimed.2022.114818. Epub 2022 Feb 16. Soc Sci Med. 2022. PMID: 35247782 Free PMC article.
-
Reframing Optimal Control Problems for Infectious Disease Management in Low-Income Countries.Bull Math Biol. 2023 Mar 12;85(4):31. doi: 10.1007/s11538-023-01137-4. Bull Math Biol. 2023. PMID: 36907932 Free PMC article.
-
Comparing optimization criteria in antibiotic allocation protocols.R Soc Open Sci. 2022 Mar 23;9(3):220181. doi: 10.1098/rsos.220181. eCollection 2022 Mar. R Soc Open Sci. 2022. PMID: 35345436 Free PMC article.
-
The potential application of probiotics and prebiotics for the prevention and treatment of COVID-19.NPJ Sci Food. 2020 Oct 5;4:17. doi: 10.1038/s41538-020-00078-9. eCollection 2020. NPJ Sci Food. 2020. PMID: 33083549 Free PMC article. Review.
-
A Refunding Scheme to Incentivize Narrow-Spectrum Antibiotic Development.Bull Math Biol. 2022 Apr 22;84(6):59. doi: 10.1007/s11538-022-01013-7. Bull Math Biol. 2022. PMID: 35451653 Free PMC article.
References
-
- Aleman DM, Wibisono TG, Schwartz B (2009) Accounting for individual behaviors in a pandemic disease spread model. Winter Simulation Conference, 1977–1985 (Winter Simulation Conference).
-
- Alirol E, Wi TE, Bala M, Bazzo ML, Chen XS, Deal C, Dillon JAR, Kularatne R, Heim J, Hooft van Huijsduijnen R, Hook EW, Lahra MM, Lewis DA, Ndowa F, Shafer WM, Tayler L, Workowski K, Unemo M, Balasegaram M (2017) Multidrug-resistant gonorrhea: A research and development roadmap to discover new medicines. PLoS Medicine 14(7):1–12. - PMC - PubMed
-
- Ambrosch A, Rockmann F (2016) Effect of two-step hygiene management on the prevention of nosocomial influenza in a season with high influenza activity. Journal of Hospital Infection 94(2):143–149. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
