Nonlinear material and ionic transport through membrane nanotubes
- PMID: 34118214
- PMCID: PMC8438788
- DOI: 10.1016/j.bbamem.2021.183677
Nonlinear material and ionic transport through membrane nanotubes
Abstract
Membrane nanotubes (NTs) and their networks play an important role in intracellular membrane transport and intercellular communications. The transport characteristics of the NT lumen resemble those of conventional solid-state nanopores. However, unlike the rigid pores, the soft membrane wall of the NT can be deformed by forces driving the transport through the NT lumen. This intrinsic coupling between the NT geometry and transport properties remains poorly explored. Using synchronized fluorescence microscopy and conductance measurements, we revealed that the NT shape was changed by both electric and hydrostatic forces driving the ionic and solute fluxes through the NT lumen. Far from the shape instability, the strength of the force effect is determined by the lateral membrane tension and is scaled with membrane elasticity so that the NT can be operated as a linear elastic sensor. Near shape instabilities, the transport forces triggered large-scale shape transformations, both stochastic and periodic. The periodic oscillations were coupled to a vesicle passage along the NT axis, resembling peristaltic transport. The oscillations were parametrically controlled by the electric field, making NT a highly nonlinear nanofluidic circuitry element with biological and technological implications.
Keywords: Electro-actuation; Membrane elasticity; Membrane nanotube; Nanofluidic transport; Shape bistability.
Copyright © 2021 Elsevier B.V. All rights reserved.
Conflict of interest statement
Declaration of interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Figures
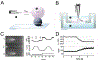
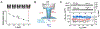
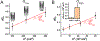
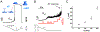
Similar articles
-
Self-assembling organic nanotubes with precisely defined, sub-nanometer pores: formation and mass transport characteristics.Acc Chem Res. 2013 Dec 17;46(12):2856-66. doi: 10.1021/ar400030e. Epub 2013 Apr 18. Acc Chem Res. 2013. PMID: 23597055 Review.
-
Nanotubes connecting B lymphocytes: High impact of differentiation-dependent lipid composition on their growth and mechanics.Biochim Biophys Acta Mol Cell Biol Lipids. 2017 Sep;1862(9):991-1000. doi: 10.1016/j.bbalip.2017.06.011. Epub 2017 Jun 20. Biochim Biophys Acta Mol Cell Biol Lipids. 2017. PMID: 28645851
-
Asymmetric ion transport through ion-channel-mimetic solid-state nanopores.Acc Chem Res. 2013 Dec 17;46(12):2834-46. doi: 10.1021/ar400024p. Epub 2013 May 28. Acc Chem Res. 2013. PMID: 23713693 Review.
-
Nanotechnological selection.Nanotechnology. 2013 Jan 18;24(2):020201. doi: 10.1088/0957-4484/24/2/020201. Epub 2012 Dec 14. Nanotechnology. 2013. PMID: 23242125
-
Nonlinear electrohydrodynamic ion transport in graphene nanopores.Sci Adv. 2022 Jan 14;8(2):eabj2510. doi: 10.1126/sciadv.abj2510. Epub 2022 Jan 14. Sci Adv. 2022. PMID: 35030026 Free PMC article.
Cited by
-
Membrane Lipid Reshaping Underlies Oxidative Stress Sensing by the Mitochondrial Proteins UCP1 and ANT1.Antioxidants (Basel). 2022 Nov 23;11(12):2314. doi: 10.3390/antiox11122314. Antioxidants (Basel). 2022. PMID: 36552523 Free PMC article.
-
Molecular Shape Solution for Mesoscopic Remodeling of Cellular Membranes.Annu Rev Biophys. 2022 May 9;51:473-497. doi: 10.1146/annurev-biophys-011422-100054. Epub 2022 Mar 3. Annu Rev Biophys. 2022. PMID: 35239417 Free PMC article. Review.
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

