Interfacial spin-orbit torques
- PMID: 34121763
- PMCID: PMC8194107
- DOI: 10.1063/5.0024019
Interfacial spin-orbit torques
Abstract
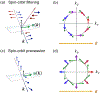
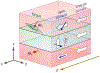
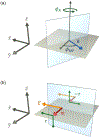
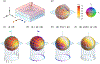
Spin-orbit torques offer a promising mechanism for electrically controlling magnetization dynamics in nanoscale heterostructures. While spin-orbit torques occur predominately at interfaces, the physical mechanisms underlying these torques can originate in both the bulk layers and at interfaces. Classifying spin-orbit torques based on the region that they originate in provides clues as to how to optimize the effect. While most bulk spin-orbit torque contributions are well studied, many of the interfacial contributions allowed by symmetry have yet to be fully explored theoretically and experimentally. To facilitate progress, we review interfacial spin-orbit torques from a semiclassical viewpoint and relate these contributions to recent experimental results. Within the same model, we show the relationship between different interface transport parameters. For charges and spins flowing perpendicular to the interface, interfacial spin-orbit coupling both modifies the mixing conductance of magnetoelectronic circuit theory and gives rise to spin memory loss. For in-plane electric fields, interfacial spin-orbit coupling gives rise to torques described by spin-orbit filtering, spin swapping and precession. In addition, these same interfacial processes generate spin currents that flow into the non-magnetic layer. For in-plane electric fields in trilayer structures, the spin currents generated at the interface between one ferromagnetic layer and the non-magnetic spacer layer can propagate through the non-magnetic layer to produce novel torques on the other ferromagnetic layer.
Figures







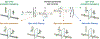
References
-
- Apalkov D, Dieny B, and Slaughter J, Proceedings of the IEEE 104, 1796 (2016).
-
- Hanyu T, Endoh T, Suzuki D, Koike H, Ma Y, Onizawa N, Natsui M, Ikeda S, and Ohno H, Proceedings of the IEEE 104, 1844 (2016).
-
- Butler W, Zhang X-G, Schulthess T, and MacLaren J, Physical Review B 63, 054416 (2001).
-
- Parkin SS, Kaiser C, Panchula A, Rice PM, Hughes B, Samant M, and Yang S-H, Nature materials 3, 862 (2004). - PubMed
-
- Yuasa S, Nagahama T, Fukushima A, Suzuki Y, and Ando K, Nature materials 3, 868 (2004). - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
